题目内容
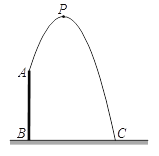
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,AE和过点C的切线互相垂直,垂足为E,AE交⊙O于点D,直线EC交AB的延长线于点P,连接AC,BC.
(1)求证:AC平分∠BAD;
(2)若AB=6,AC=4![]() ,求EC和PB的长.
,求EC和PB的长.

【答案】(1)答案见解析;(2)EC=![]() ,PB=
,PB=![]() .
.
【解析】分析:(1)首先连接OC,由PE是 O的切线,AE和过点C的切线互相垂直,可证得OC∥AE,又由OA=OC,易证得∠DAC=∠OAC,即可得AC平分∠BAD;(2)由Rt△ABC∽Rt△ACE得出CE的值,再由Rt△ABC∽Rt△ACE,得出PB的值.
本题解析:
(1)证明:连接OC,∵PE是⊙O的切线,∴OC⊥PE,∵AE⊥PE,∴OC∥AE,∴∠DAC=∠OCA,∵OA=OC,∴∠OCA=∠OAC,∴∠DAC=∠OAC,∴AC平分∠BAD;
(2)∵AB是⊙O的直径,∠ACB=90°

在Rt△ABC中,AB=6,AC=4![]() ,∴BC=
,∴BC=![]() ,在Rt△ABC和Rt△ACE中,∵∠DAC=∠OAC,∠AEC=∠ACB=90°,∴Rt△ABC∽Rt△ACE,∴
,在Rt△ABC和Rt△ACE中,∵∠DAC=∠OAC,∠AEC=∠ACB=90°,∴Rt△ABC∽Rt△ACE,∴![]() ,∴
,∴![]() ,∴EC=
,∴EC=![]()
在Rt△ACE中,AE=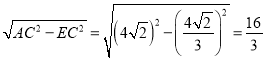 ,OC=
,OC=![]() =3
=3
又∵OC∥AE,∴Rt△ABC∽Rt△ACE,∴![]() ,∴
,∴ 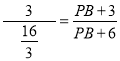 ,解得:PB=
,解得:PB=![]()

练习册系列答案
相关题目