题目内容

【题目】如图，点在抛物线上，且抛物线与轴分别交于点和点，与轴交于点

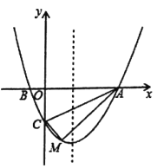
（1）求抛物线的解析式.

（2）若点为抛物线对称轴上的一个动点，求的最小值.

（3）点为抛物线上除点外的一点，若与的面积相等，求点的坐标。

【答案】(1) ;(2);(3) ，，.

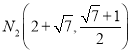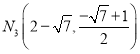【解析】

（1）将点的坐标代入求解即可.

（2）找对称点，利用两点之间线段最短求解即可.

（3）将几何问题转化为函数问题求解即可.

解（1）将点和代入得

解得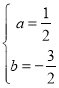

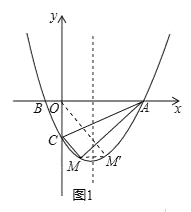
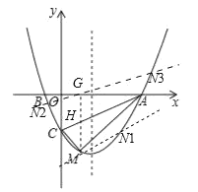
（2）如图1，作点关于对称轴的对称点，连接

则的最小值为

∵，∴最小值为

（3）由（1）可求出，

∴直线的解析式为

∵与的面积相等

∴

如图所示：①过作交抛物线于点

∵

∴直线的解析式为

联合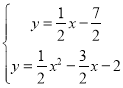

得或

∴

②过点作，交抛物线于点

直线的解析式为

联合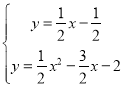

解得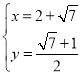或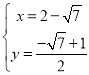

∴，

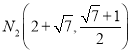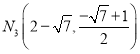
综上所述，满足条件的有三个，分别为：

，，

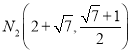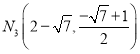
练习册系列答案
相关题目

【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

（1）求证：ED为⊙O的切线；

（2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

试题解析：(1)证明：连接OD，

∵OE∥AB，

∴∠COE=∠CAD，∠EOD=∠ODA，

∵OA=OD,

∴∠OAD=∠ODA，

∴∠COE=∠DOE，

在△COE和△DOE中，

∴△COE≌△DOE(SAS)，

∴ED⊥OD，

∴ED是的切线；

(2)连接CD，交OE于M，

在Rt△ODE中，

∵OD=32，DE=2，

∵OE∥AB，

∴△COE∽△CAB，

∴AB=5，

∵AC是直径，

∵EF∥AB，

∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为

【题型】解答题
【结束】
25

【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．

（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；

（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；

（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．

【题目】已知一个口袋中装有六个完全相同的小球，小球上分别标有1，2，5，7，8，13六个数，搅匀后一次从中摸出一个小球，将小球上的数记为m，则使得一次函数y＝（﹣m+1）x+11﹣m经过一、二、四象限且关于x的分式方程＝3x+的解为整数的概率是（　　）

A.B.C.D.

【题目】关于x的一元二次方程x2+（2k+1）x+k2+1=0有两个不等实根x1、x2．

（1）求实数k的取值范围．

（2）若方程两实根x1、x2满足x1+x2=﹣x1x2，求k的值．

【题目】如图，已知△ABC，以AC为直径的⊙O交AB于点D，点E为弧AD的中点，连接CE交AB于点F，且BF=BC．

（1）求证：BC是⊙O的切线；

（2）若⊙O的半径为2，=，求CE的长．

【题目】如图，在△ABC中，∠B＝42°，把△ABC绕着点A顺时针旋转，得到△AB'C'，点C的对应点C'落在BC边上，且B'A∥BC，则∠BAC'的度数为（　　）

A.24°B.25°C.26°D.27°

【题目】如图，四边形ABCD是正方形，E是AD边上的一个动点（有与A、D重合），以E为圆心，EA为半径的⊙E交CE于G点，CF与⊙E切于F点．AD＝4，AE＝x，CF2＝y．

（1）求y与x的函数关系式，并写出x的取值范围；

（2）是否存在x的值，使得FG把△CEF的面积分成1：2两部分？若存在，求出x的值；若不存在，请说明理由．

【题目】已知在半径为3的⊙O中，弦AB=3，弦AC=3，则∠BAC的度数为________.

【题目】对于给定的图形G和点P，若点P可通过一次向上或向右平移n（n＞0）个单位至图形G上某点P′，则称点P为图形G的“可达点”，特别地，当点P在图形G上时，点P为图形G的“可达点”．

（1）如图1，在平面直角坐标系xOy中，点A（1，1），B（2，1），

①在点O、A、B中，不是直线y＝﹣x+2的“可达点”的是　 　；

②若点A是直线l的“可达点”且点A不在直线l上，写出一条满足要求的直线l的表达式：　 　；

③若点A、B中有且仅有一点是直线y＝kx+2的“可达点”，则k的取值范围是　 　．

（2）如图2，在平面直角坐标系xOy中，⊙O的半径为1，直线l：y＝﹣x+b．

①当b＝﹣2时，若直线m上一点N（xN，yN）满足N是⊙O的“可达点”，直接写出xN的取值范围　 　；

②若直线m上所有的⊙O的“可达点”构成一条长度不为0的线段，直接写出b的取值范围　 　．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网