题目内容
当∠A+∠B=90°时,下列结论错误的是
- A.cosA=sinB
- B.sinA=cosB
- C.sinA=cos(90°-A)
- D.sin(90°-A)=sinA
D
分析:根据三角函数的定义得出各角三角函数值,从而得出若∠A+∠B=90°,那么sinA=cos(90°-A),sinA=cosB或sinB=cosA,即可得出答案.
解答: 解:A.∵cosA=
解:A.∵cosA= ,sinB=
,sinB= ,
,
∴cosA=sinB,故选项A正确;
B.∵sinA= ,cosB=
,cosB= ,
,
∴sinA=cosB,故选项B正确;
C.∵sinA= ,cos(90°-A)=cosB=
,cos(90°-A)=cosB= ,
,
∴sinA=cos(90°-A),故选项C正确;
D.∵sin(90°-A)=sinB= ,sinA=
,sinA= ,
,
∴sin(90°-A)≠sinA,故D选项错误.
故选:D.
点评:此题主要考查了互余两角三角函数的关系,根据两角关系画出直角三角形得出各三角函数值是解题关键.
分析:根据三角函数的定义得出各角三角函数值,从而得出若∠A+∠B=90°,那么sinA=cos(90°-A),sinA=cosB或sinB=cosA,即可得出答案.
解答:
 解:A.∵cosA=
解:A.∵cosA= ,sinB=
,sinB= ,
,∴cosA=sinB,故选项A正确;
B.∵sinA=
 ,cosB=
,cosB= ,
,∴sinA=cosB,故选项B正确;
C.∵sinA=
 ,cos(90°-A)=cosB=
,cos(90°-A)=cosB= ,
,∴sinA=cos(90°-A),故选项C正确;
D.∵sin(90°-A)=sinB=
 ,sinA=
,sinA= ,
,∴sin(90°-A)≠sinA,故D选项错误.
故选:D.
点评:此题主要考查了互余两角三角函数的关系,根据两角关系画出直角三角形得出各三角函数值是解题关键.

练习册系列答案
相关题目

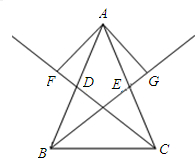 如图,已知△ABC中,AB=AC,∠A<90°,CD、BE分别为△ABC的中线,AF⊥CD,AG⊥BE,分别交CD、BE的延长线于F、G两点,试问:
如图,已知△ABC中,AB=AC,∠A<90°,CD、BE分别为△ABC的中线,AF⊥CD,AG⊥BE,分别交CD、BE的延长线于F、G两点,试问: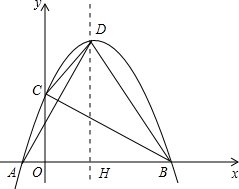 侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
侧),与y轴相交于点C,顶点D在第一象限.过点D作x轴的垂线,垂足为H.
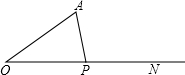 如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=30°,当∠A=
如图,已知点P是射线ON上一动点(即P可在射线ON上运动),∠AON=30°,当∠A=