题目内容
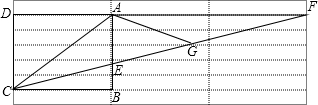
“三等分一个任意角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的.在探索中,有人曾利用过如图所示的图形,其中,ABCD是长方形,F是DA延长线上一点,G是CF上一点,并且∠ACG=∠AGC,∠GAF=∠F.
(1)探索∠ECB和∠ACB的数量关系,并证明你的结论.
(2)若∠ACG=40度,GF=4,求长方形ABCD的周长.
(1)探索∠ECB和∠ACB的数量关系,并证明你的结论.
(2)若∠ACG=40度,GF=4,求长方形ABCD的周长.

考点:矩形的性质,等腰三角形的判定与性质,含30度角的直角三角形,勾股定理
专题:
分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AGC=2∠F,从而得到∠ACG=2∠F,根据两直线平行,内错角相等可得∠ECB=∠F,再求出∠ACB=3∠F,从而得解;
(2)先求出∠ACB=60°,再根据等角对等边可得AC=AG=GF,然后求出AB、BC,再根据矩形的周长的定义列式计算即可得解.
(2)先求出∠ACB=60°,再根据等角对等边可得AC=AG=GF,然后求出AB、BC,再根据矩形的周长的定义列式计算即可得解.
解答:解:(1)∠ACB=3∠ECB.
理由如下:在△AGF中,∠AGC=∠F+∠GAF=2∠F,
∵∠ACG=∠AGC,
∴∠ACG=2∠F,
∵AD∥BC,
∴∠ECB=∠F,
∴∠ACB=∠ACG+∠BCE=3∠F,
故∠ACB=3∠ECB;
(2)∵∠ACG=40°,
∴∠F=
×40°=20°,
∴∠ACB=3×20°=60°,
∵∠ACG=∠AGC,∠GAF=∠F,
∴AC=AG=GF=4,
∴AB=4×
=2
,BC=4×
=2,
∴长方形ABCD的周长=2(AB+BC)=2(2
+2)=4
+4.
理由如下:在△AGF中,∠AGC=∠F+∠GAF=2∠F,
∵∠ACG=∠AGC,
∴∠ACG=2∠F,
∵AD∥BC,
∴∠ECB=∠F,
∴∠ACB=∠ACG+∠BCE=3∠F,
故∠ACB=3∠ECB;
(2)∵∠ACG=40°,
∴∠F=
| 1 |
| 2 |
∴∠ACB=3×20°=60°,
∵∠ACG=∠AGC,∠GAF=∠F,
∴AC=AG=GF=4,
∴AB=4×
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴长方形ABCD的周长=2(AB+BC)=2(2
| 3 |
| 3 |
点评:本题考查了矩形的性质,等角对等边的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,解直角三角形,熟记各性质并读懂题目信息理解三等分角的方法是解题的关键.

练习册系列答案
 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
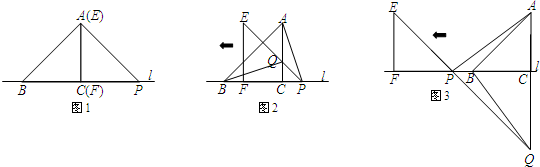
 已知在Rt△ABC中,∠C=90°,AC=BC=2.将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交线段AC、CB于D、E两点.如图1、2是旋转三角板得到的图形中的两种情况.
已知在Rt△ABC中,∠C=90°,AC=BC=2.将一块等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交线段AC、CB于D、E两点.如图1、2是旋转三角板得到的图形中的两种情况.