题目内容
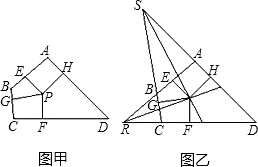
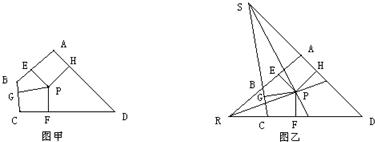
18、定义:到四边形一组对边距离相等,到另一组对边的距离也相等的点叫做这个四边形的准内点.如图甲,PE=PF,PG=PH,则点P就是四边形ABCD的准内点.
如图乙,∠ARD与∠CSD的角平分线相交于点P,根据角平分线的性质可以得出点P是就是四边形ABCD的准内点.
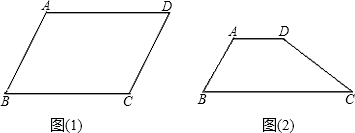
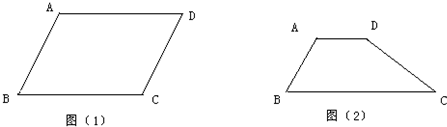
请你分别画出平行四边形(图1)和梯形(图2)的准内点,并简要说明准内点的位置.
画图:
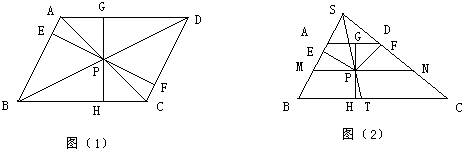
说明:
(1)
(2)
如图乙,∠ARD与∠CSD的角平分线相交于点P,根据角平分线的性质可以得出点P是就是四边形ABCD的准内点.

请你分别画出平行四边形(图1)和梯形(图2)的准内点,并简要说明准内点的位置.

画图:

说明:
(1)
对角线AC、BD的交点P即为平行四边形ABCD的准内点
.(2)
∠BSC的角平分线ST与梯形中位线MN的交点P即为梯形ABCD的准内点
.分析:如图(1)只要证得PJ=PH,PG=PI,即可得出结论;通过证明△PEJ≌△PEH和△PGF≌△PIF即可得出;
(2)根据平行四边形的性质,对角线互相平分,可得出交点既是准内心,根据角平分线的性质定理和梯形中位线的性质定理,可得梯形两腰夹角的平分线与梯形中位线的交点即为准内心,
(2)根据平行四边形的性质,对角线互相平分,可得出交点既是准内心,根据角平分线的性质定理和梯形中位线的性质定理,可得梯形两腰夹角的平分线与梯形中位线的交点即为准内心,
解答: 解:(1)证明:作PI⊥FD,PJ⊥DE,PG⊥AF,PH⊥EC,
解:(1)证明:作PI⊥FD,PJ⊥DE,PG⊥AF,PH⊥EC,
∵EP平分∠DEC,
∴∠PED=∠CEP,
在△PEJ和△PEH中,
∠PED=∠CEP,PE=PE,∠PHE=∠PJE,
∴△PEJ≌△PEH,
∴PJ=PH,
同理,可证△PGF≌△PIF,
∴PG=PI,
∴点P是四边形ABCD的准内心;
(2)平行四边形对角线AC、BD的交点P1就是准内心,如图3(1),
或者取平行四边形两对边中点连线的交点P1就是准内心,如图3(2),
梯形两腰夹角的平分线与梯形中位线的交点P2就是准内心,如图4.
 解:(1)证明:作PI⊥FD,PJ⊥DE,PG⊥AF,PH⊥EC,
解:(1)证明:作PI⊥FD,PJ⊥DE,PG⊥AF,PH⊥EC,∵EP平分∠DEC,
∴∠PED=∠CEP,
在△PEJ和△PEH中,
∠PED=∠CEP,PE=PE,∠PHE=∠PJE,
∴△PEJ≌△PEH,

∴PJ=PH,
同理,可证△PGF≌△PIF,
∴PG=PI,
∴点P是四边形ABCD的准内心;
(2)平行四边形对角线AC、BD的交点P1就是准内心,如图3(1),
或者取平行四边形两对边中点连线的交点P1就是准内心,如图3(2),
梯形两腰夹角的平分线与梯形中位线的交点P2就是准内心,如图4.
点评:本题主要考查了多边形的准内心,用到的知识点是角平分线、中位线的性质定理;可通过证明三角形全等来证得结论,难度适中.

练习册系列答案
相关题目