Question

有4张正面分别标有数字0，1，2，3的不透明卡片，它们除数字不同外其余都相同．现将它们背面朝上，洗匀后任选两张，将这两张卡片上的数分别记为m、n的值，记点P（m，n），则点P落在直线y=x（x≥0）与直线y=-x+4（x≥0）和x轴围成的三角形内（含三角形边界）概率是________．

Answer 1

分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与点P落在直线y=x（x≥0）与直线y=-x+4（x≥0）和x轴围成的三角形内（含三角形边界）的情况，再利用概率公式求解即可求得答案．
解答：画树状图得：

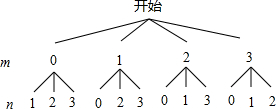
∵共有12种等可能的结果，点P落在直线y=x（x≥0）与直线y=-x+4（x≥0）和x轴围成的三角形内（含三角形边界）有：（1，0），（2，0），（2，1），（3，0），（3，1），
∴点P落在直线y=x（x≥0）与直线y=-x+4（x≥0）和x轴围成的三角形内（含三角形边界）概率是：5÷12=．
故答案为：．
点评：本题考查的是用列表法或画树状图法求概率与一次函数的性质．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．注意概率=所求情况数与总情况数之比．