题目内容
【题目】甲、乙两车从![]() 城出发前往
城出发前往![]() 城,在整个行程中,汽车离开
城,在整个行程中,汽车离开![]() 城的距离
城的距离![]() 与时刻
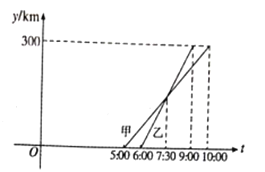
与时刻![]() 的对应关系如右图所示.
的对应关系如右图所示.
(1)![]() 、
、![]() 两城相距多远?
两城相距多远?
(2)哪辆车先出发?哪辆车先到![]() 城?
城?
(3)甲、乙两车的平均速度分别为多少?
(4)你还能从图中得到哪些信息?
【答案】(1)![]() ;(2)甲先出发,乙先到达;(3)甲
;(2)甲先出发,乙先到达;(3)甲![]() ,乙
,乙![]() ; (4)
; (4)![]() 甲在乙前或
甲在乙前或![]() 乙追上甲或
乙追上甲或![]() 乙在甲前.(只要合理均可给分)
乙在甲前.(只要合理均可给分)
【解析】
(1)根据图示知,纵坐标表示汽车离开A城的距离,所以A,B两城相距300米;
(2)根据甲、乙两车的出发时间和到达时间进行回答;
(3)速度=![]() ,依此列式计算即可求解.
,依此列式计算即可求解.
(4)根据图象得出其他信息即可.
解:(1)由图示知:A,B两城相距300km;
(2)由图示知,甲车从5:00出发,乙车从6:00出发;甲车10:00到达B城,乙车9:00到达B城.
答:甲车先出发,乙车先到达B城;
(3)如图所示:甲车的平均速度为![]() ,乙车的平均速度为:
,乙车的平均速度为:![]() ,
,
答:甲、乙两车的平均速度分别是60km/h、100km/h.
(4)300-60×4=60(千米),
答:乙车到达B城时,甲车距离B城的距离60千米.
故答案为:300;60:100.

 阅读快车系列答案
阅读快车系列答案【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.