题目内容
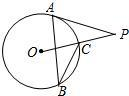如图，PA切⊙O于A，OP交⊙O于C，B为⊙O上的点，连接AB，BC．若∠P=20°，则∠B=________度．
35
分析：连接OA，根据切线的性质定理得OA⊥AP，则∠AOP=90°-∠P=70°，再根据一条弧所对的圆周角等于它所对的圆心角的一半即可求出∠B．
解答：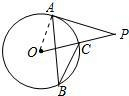
解：如图，连接OA，
∵PA切⊙O于A，
∴OA⊥AP，
∴∠AOP=90°-∠P=70°，
∴∠B=
∠AOP=35°．
点评：此题综合运用了切线的性质以及圆周角定理解决问题．
分析：连接OA，根据切线的性质定理得OA⊥AP，则∠AOP=90°-∠P=70°，再根据一条弧所对的圆周角等于它所对的圆心角的一半即可求出∠B．
解答：
解：如图，连接OA，∵PA切⊙O于A，
∴OA⊥AP，
∴∠AOP=90°-∠P=70°，
∴∠B=
∠AOP=35°．点评：此题综合运用了切线的性质以及圆周角定理解决问题．
练习册系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
第三学期赢在暑假系列答案
相关题目
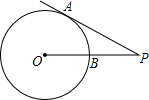如图，PA切⊙O于点A，PO交⊙O于点B，若PA=6，BP=4，则⊙O的半径为（ ）A、
| ||
B、
| ||
| C、2 | ||
| D、5 |
如图，PA切⊙O于点A，PBC是⊙O的割线，且PB=BC，如果PA=3| 2 |
A、3
| ||
| B、3 | ||
C、
| ||
D、2
|
8、如图，PA切⊙O于点A，PBC是⊙O的割线且过圆心，PA=4，PB=2，则⊙O的半径等于（ ）
如图，PA切⊙O于点A，PB切⊙O于点B，如果∠APB=60°，⊙O半径是3，则劣弧AB的长为（ ）A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
如图：PA切⊙O于A，PB切⊙O于B，OP交⊙O于C，下列结论中错误的是（ ）