题目内容
 某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙长20米),另外三边用篱笆围成如图所示,所用的篱笆长为36米.
某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙长20米),另外三边用篱笆围成如图所示,所用的篱笆长为36米.(1)设垂直于墙的一边长为x米.则平行于墙的一边为
(36-2x)
(36-2x)
米;(2)当花圃的面积为144平方米时,求垂直于墙的一边的长为多少米?
分析:(1)设垂直于墙的一边长为x米.则平行于墙的一边长根据总长减去垂直于墙的两边的边长为2x米就得出(36-2x)米;
(2)根据(1)由矩形的面积公式可以得出x(36-2x)=144,求出其解就可以得出结论.
(2)根据(1)由矩形的面积公式可以得出x(36-2x)=144,求出其解就可以得出结论.
解答:解:(1)设垂直于墙的一边长为x米.由题意,得
平行于墙的一边长为:(36-2x)米,
故答案为:36-2x.
(2)设垂直于墙的一边长为x米,则平行于墙的一边长为(36-2x)米,由题意,得
x(36-2x)=144,
解得:x1=6,x2=12,
,36-2x≤20,
∴x≥8,
∴x=6不符合题意,应舍去,
∴
x=12.
答:垂直于墙的一边的长为12米.
平行于墙的一边长为:(36-2x)米,
故答案为:36-2x.
(2)设垂直于墙的一边长为x米,则平行于墙的一边长为(36-2x)米,由题意,得
x(36-2x)=144,
解得:x1=6,x2=12,
,36-2x≤20,
∴x≥8,
∴x=6不符合题意,应舍去,
∴
x=12.
答:垂直于墙的一边的长为12米.
点评:本题是一道关于一元二次方程的运用的实际问题的运用题,考查了一元二次方程的解法的运用,矩形的面积公式的运用,在解答时根据矩形的面积建立方程是关键.

练习册系列答案
相关题目
 某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成(如图所示).
某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成(如图所示). 某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成(如图所示).
某园艺公司准备围建一个矩形花圃,其中一边靠墙(墙足够长),另外三边用篱笆围成(如图所示). 阅读材料:
阅读材料: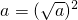 .如:2=
.如:2= ,
,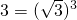 等.
等.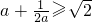 .
.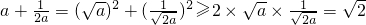
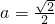 时,等号成立.
时,等号成立. .如:2=
.如:2= ,
, 等.
等. .
.
 ,当且仅当
,当且仅当 时,等号成立.
时,等号成立.