题目内容
 (2006•河北区一模)如图,已知二次函数的顶点坐标为(2,0),直线y=x+2与该二次函数的图象交于A,B两点,其中A点在y轴上,
(2006•河北区一模)如图,已知二次函数的顶点坐标为(2,0),直线y=x+2与该二次函数的图象交于A,B两点,其中A点在y轴上,(I)求此二次函数的解析式.
(II)P为线段AB上一点(A,B两端点除外),过P点作x轴的垂线PC与(I)中的二此函数的图象交于Q点,设线段PQ的长为m,P点的横坐标为x,求出函数m与自变量x之间的函数关系式,并求出自变量x的取值范围.
(III)线段AB上是否存在一点,使(II)中的线段PQ的长等于5?若存在,求出P点的坐标;若不存在,请说明理由.
分析:(Ⅰ)已知抛物线的顶点坐标,可将该抛物线的解析式设为顶点式,要想用待定系数法求出抛物线的解析式,还需找出另外一点的坐标,显然直线AB与y轴的交点A是最好的选择,按此思路求解即可.
(Ⅱ)根据给出的P点横坐标,结合直线AB和抛物线的解析式,先表示出P、Q两点的坐标,它们纵坐标的差即为线段PQ的长.自变量的取值范围可由A、B两点的坐标来确定.
(Ⅲ)将PQ的长代入上题的函数解析式中,能得到一个方程,若方程有解即可得到符合条件的P点坐标;若方程无解,那么就不存在符合条件的P点.
(Ⅱ)根据给出的P点横坐标,结合直线AB和抛物线的解析式,先表示出P、Q两点的坐标,它们纵坐标的差即为线段PQ的长.自变量的取值范围可由A、B两点的坐标来确定.
(Ⅲ)将PQ的长代入上题的函数解析式中,能得到一个方程,若方程有解即可得到符合条件的P点坐标;若方程无解,那么就不存在符合条件的P点.
解答:解:(Ⅰ)由直线AB:y=x+2 知,A(0,2);
已知抛物线的顶点坐标为(2,0),可设其解析式为 y=a(x-2)2,代入A点坐标得:
2=a(0-2)2,a=
∴抛物线的解析式:y=
(x-2)2=
x2-2x+2.
(Ⅱ)已知点P的横坐标为x,则P(x,x+2)、Q(x,
x2-2x+2);
则:PQ=(x+2)-(
x2-2x+2)=-
x2+3x
由于点P在线段AB上移动,且不与A、B重合,所以 0<x<6;
综上,m=-
x2+3x,0<x<6,
(Ⅲ)不存在.
理由:将PQ=5代入(Ⅱ)的函数解析式中,得:
5=-
x2+3x,化简得:x2-6x+10=0
△=36-40<0
∴不存在符合条件的P点.
已知抛物线的顶点坐标为(2,0),可设其解析式为 y=a(x-2)2,代入A点坐标得:
2=a(0-2)2,a=
| 1 |
| 2 |
∴抛物线的解析式:y=
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)已知点P的横坐标为x,则P(x,x+2)、Q(x,
| 1 |
| 2 |
则:PQ=(x+2)-(
| 1 |
| 2 |
| 1 |
| 2 |
由于点P在线段AB上移动,且不与A、B重合,所以 0<x<6;
综上,m=-
| 1 |
| 2 |
(Ⅲ)不存在.
理由:将PQ=5代入(Ⅱ)的函数解析式中,得:
5=-
| 1 |
| 2 |
△=36-40<0
∴不存在符合条件的P点.
点评:该题是较为简单的二次函数综合题,只要准确得到抛物线的解析式,后面的题目就能迎刃而解.第二小题要注意点的运动范围,以便正确的得到自变量的取值范围.

练习册系列答案
相关题目
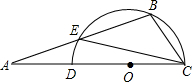 (2006•河北区一模)如图,DC是半圆O的直径,若∠A=20°,∠BCE=40°,则∠BEC等于( )
(2006•河北区一模)如图,DC是半圆O的直径,若∠A=20°,∠BCE=40°,则∠BEC等于( )