题目内容
如图，抛物线y=x2-2x-3与x轴交于A、B两点，与y轴交于点C．
（1）点A的坐标为________，点B的坐标为________，点C的坐标为________．
（2）设抛物线y=x2-2x-3的顶点为M，求四边形ABMC的面积．
（1）解：当y=0时，x2-2x-3=0，
解得：x1=3，x2=-1，
∴点A的坐标是（-1，0），点B的坐标是（3，0），
当x=0时，y=-3，
∴点C的坐标是（0，-3），
故答案为：（-1，0），（3，0），（0，-3）；
（2）解：y=x2-2x-3=（x-1）2-4，
∴M（1，-4），
过M作MN⊥X轴于N，
则：ON=1，MN=4，BN=3-1=2，OA=1，OC=3，
∴四边形ABMC的面积S=S△COA+S梯形CONM+S△BNM，
=
OA×OC+×（OC+MN）×ON+×MN×BN
=×1×3+×（3+4）×1+×2×4，
=9．
答：四边形ABMC的面积是9．
分析：（1）把y=0和x=0分别代入解析式即可求出A、B、C的坐标；
（2）把解析式化成顶点式即可求出M的坐标，过M作MN⊥X轴于N，这样四边形ACMB的面积就转化成△ACO、梯形OCMN、△BMN的面积，根据点的坐标求出各个面积代入即可．
点评：本题主要考查了二次函数上点的坐标特点，三角形和梯形的面积等知识点，解此题的关键是通过作辅助线把不规则的四边形转化成规则的图形．题型较好，比较典型．
解得：x1=3，x2=-1，
∴点A的坐标是（-1，0），点B的坐标是（3，0），
当x=0时，y=-3，
∴点C的坐标是（0，-3），
故答案为：（-1，0），（3，0），（0，-3）；
（2）解：y=x2-2x-3=（x-1）2-4，
∴M（1，-4），
过M作MN⊥X轴于N，
则：ON=1，MN=4，BN=3-1=2，OA=1，OC=3，
∴四边形ABMC的面积S=S△COA+S梯形CONM+S△BNM，
=
OA×OC+×（OC+MN）×ON+×MN×BN=
×1×3+×（3+4）×1+×2×4，=9．
答：四边形ABMC的面积是9．
分析：（1）把y=0和x=0分别代入解析式即可求出A、B、C的坐标；
（2）把解析式化成顶点式即可求出M的坐标，过M作MN⊥X轴于N，这样四边形ACMB的面积就转化成△ACO、梯形OCMN、△BMN的面积，根据点的坐标求出各个面积代入即可．
点评：本题主要考查了二次函数上点的坐标特点，三角形和梯形的面积等知识点，解此题的关键是通过作辅助线把不规则的四边形转化成规则的图形．题型较好，比较典型．
练习册系列答案
相关题目
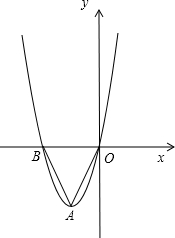如图，抛物线y=x2+4x与x轴分别相交于点B、O，它的顶点为A，连接AB，AO．
16、如图，抛物线y=-x2+2x+m（m＜0）与x轴相交于点A（x1，0）、B（x2，0），点A在点B的左侧．当x=x2-2时，y
已知如图，抛物线y=x2+（k2+1）x+k+1的对称轴是直线x=-1，且顶点在x轴上方．设M是直线x=-1左侧抛物线上的一动点，过点M作x轴的垂线MG，垂足为G，过点M作直线x=-1的垂线MN，垂足为N，直线x=-1与x轴的交于H点，若M点的横坐标为x，矩形MNHG的周长为l．
（2013•扬州）如图，抛物线y=x2-2x-8交y轴于点A，交x轴正半轴于点B．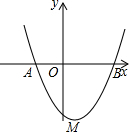
如图，抛物线y=x2-2x-3与x轴分别交于A，B两点．