题目内容
【题目】定义:如图1,抛物线 ![]() 与
与 ![]() 轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足
轴交于A,B两点,点P在抛物线上(点P与A,B两点不重合),如果△ABP的三边满足 ![]() ,则称点P为抛物线
,则称点P为抛物线 ![]() 的勾股点。
的勾股点。

(1)直接写出抛物线 ![]() 的勾股点的坐标;
的勾股点的坐标;
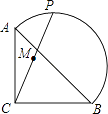
(2)如图2,已知抛物线C: ![]() 与
与 ![]() 轴交于A,B两点,点P(1,
轴交于A,B两点,点P(1, ![]() )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件 ![]() 的点Q(异于点P)的坐标
的点Q(异于点P)的坐标
【答案】
(1)
解:勾股点的坐标为(0,1)
(2)
解:抛物线y=ax2+bx(a≠0)过原点(0,0),即A(0,0),
如图作PG⊥x轴于点G,连接PA,PB,
∵点P(1,![]() ),
),
∴ AG=1,PG=![]() ,
,
∴PA=2,tan∠PAB=![]() ,
,
∴∠PAB=60°,
∴在Rt△PAB中,AB=![]() =4,
=4,
∴点B(4,0),
设y=ax(x-4),当x=1时,y=![]() ,
,
解得a=-![]() ,
,
∴y=-![]() x(x-4)=-
x(x-4)=-![]() x2+
x2+![]() x.
x.

(3)
解:① 当点Q在x轴上方,由S△ABQ=S△ABP,易知点Q的纵坐标为![]() ,
,
∴-![]() x2+
x2+![]() x=
x=![]() ,解得x1=3,x2=1(不合题意,舍去),
,解得x1=3,x2=1(不合题意,舍去),
∴Q(3,![]() ),
),
②当点Q在x轴下方,由S△ABQ=S△ABP,易知点Q的纵坐标为-![]() ,
,
∴-![]() x2+
x2+![]() x=-
x=-![]() ,解得x1=2+
,解得x1=2+![]() ,x2=2-
,x2=2-![]() ,
,
∴Q(2+![]() ,-
,-![]() )Q(2-
)Q(2-![]() ,-
,-![]() ),
),
综上,满足条件的点Q有三个:Q(3,![]() )Q(2+
)Q(2+![]() ,-
,-![]() )Q(2-
)Q(2-![]() ,-
,-![]() ).
).
【解析】(1)解:y=-x2+1与x轴交于A(-1,0),B(1,0),与y轴交于P(0,1),
∴AB=2,AP=BP=![]() ,
,
∴AP2+BP2=AB2
∴勾股点P(0,1),

 名校课堂系列答案
名校课堂系列答案【题目】将从1开始的连续自然数按图规律排列:规定位于第m行,第n列的自然数10记为(3,2),自然数15记为(4,2)…
列 行 | 第1列 | 第2列 | 第3列 | 第4列 |
第1行 | 1 | 2 | 3 | 4 |
第2行 | 8 | 7 | 6 | 5 |
第3行 | 9 | 10 | 11 | 12 |
第4行 | 16 | 15 | 14 | 13 |
… | … | … | … | … |
第n行 | … | … | … | … |
按此规律,回答下列问题:
(1)记为(6,3)表示的自然数是__________________.
(2)自然数2018记为_________________.
(3)用一个正方形方框在第span>3列和第4列中任意框四个数,这四个数的和能为2018吗?如果能,求出框出的四个数中最小的数;如果不能,请写出理由。