题目内容
如图，以正方形ABCD的一边CD为边，向形外作等边三角形CDE，连接AC、AE，则下列结论错误的是
- A.∠ACE=105°
- B.∠ADE=150°
- C.∠DEA=15°
- D.△EFC的面积大于△ACF的面积
D
分析：根据四边形ABCD是正方形，三角形CDE为等边三角形，结合其性质对每个选项分析、解答即可得出结论；
解答：根据题意，四边形ABCD是正方形，三角形CDE为等边三角形，
∴∠ACE=45°+60°=105°，
∠ADE=90°+60°=150°，
∠DEA=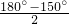
=15°；
所以，选项A、B、C正确；
∵S△ACF=
×CF×AD，S△EFC=×CF×
AD；
AD＞AD；
即△EFC的面积小于△ACF的面积；故选项D错误；
故选D．
点评：本题考查了正方形的性质和等边三角形的性质，熟练掌握其性质定理是正确解答本题的关键．
分析：根据四边形ABCD是正方形，三角形CDE为等边三角形，结合其性质对每个选项分析、解答即可得出结论；
解答：根据题意，四边形ABCD是正方形，三角形CDE为等边三角形，
∴∠ACE=45°+60°=105°，
∠ADE=90°+60°=150°，
∠DEA=
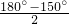=15°；所以，选项A、B、C正确；
∵S△ACF=
×CF×AD，S△EFC=×CF×AD；AD＞
AD；即△EFC的面积小于△ACF的面积；故选项D错误；
故选D．
点评：本题考查了正方形的性质和等边三角形的性质，熟练掌握其性质定理是正确解答本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
13、如图，以直角△ABC的三边向外作正方形，其面积分别为S1，S2，S3且S1=4，S2=8，则S3=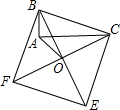
如图，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，AO=6
如图，以Rt△ABC的斜边BC为一边作正方形BCDE，设正方形的中心为O，连接AO，如果AB=3，AO=
如图，以Rt△ABC的斜边和一直角边为边长向外作正方形，面积分别为169和25，则另一直角边的长度BC为（ ）
如图，以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3，且S1+S2+S3=50，则AB=（ ）