Question

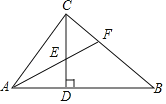
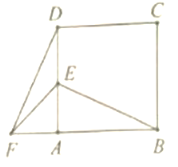
【题目】已知:如图，正方形为边上一点，绕点逆时针旋转后得到．

如果，求的度数；

与的位置关系如何?说明理由．

Answer 1

【答案】（1）20°，（2），详见解析

【解析】

（1）根据旋转的性质可知△AFD≌△AEB，则有AE＝AF，∠DAF＝90°，∠AEB＝∠DFA＝65°，然后利用∠DFE＝∠DFA－∠EFA即可求出答案．

（2）由旋转的性质得∠EBA＝∠FDA，通过等量代换即可得出∠DFA＋∠EBA＝90°，即BG⊥DF．

解：（1）根据旋转的性质可知：△AFD≌△AEB，

即AE＝AF，∠DAF＝90°，∠AEB＝∠DFA＝65°，

∴∠AFE＝45°，

∴∠DFE＝∠DFA－∠EFA＝20°

（2）延长BE与DF相交于点G．

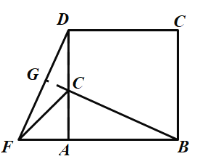
∵∠DAF＝90°，

∴∠DFA＋∠ADF＝90°，

∵∠EBA＝∠FDA，

∴∠DFA＋∠EBA＝90°，

∴BG⊥DF，即BE与DF互相垂直．