Question

【题目】如图，在矩形ABCD中，AB＝8，BC＝6，将矩形ABCD绕点A逆时针旋转得到矩形AEFG，AE，FG分别交射线CD于点P，H，连接AH，若点P是CH的中点，则△APH的周长为_____

Answer 1

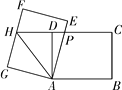
【答案】20

【解析】

设HD＝x，然后表示出HC,HP，根据等面积法得出HP＝AP，然后在Rt△APD中利用勾股定理求出x的值，进而可求出HP的长度，然后在Rt△ADH中求出HA的长度，则△APH的周长可求．

设HD＝x，由题意得HC＝x＋8．

∵点P是CH的中点，

∴HP＝＝4＋x．

由题图可知，在△HPA中，边HP和边AP上的高相等，

∴由面积法得HP＝AP．

∴AP＝4＋x．

∵DP＝HP－HD＝4－x，

∴在Rt△APD中，AP2＝DP2＋AD2．

∴(4＋x)2＝(4－x)2＋62．

解得x＝．

∴HP＝4＋×＝．

∴在Rt△ADH中，HA＝＝＝．

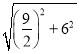∴△APH的周长为＋×2＝20．

故答案为：20．