题目内容
已知二次函数y=ax2+bx+c的图象与反比例函数![]() 的图象交于点A (a, -3),与y轴交于点B.
的图象交于点A (a, -3),与y轴交于点B.

1.(1)试确定反比例函数的解析式;
2.(2)若ÐABO =135°, 试确定二次函数的解析式;
3.(3)在(2)的条件下,将二次函数y=ax2 + bx + c的图象先沿x轴翻折, 再向右平移到与反比例函数![]() 的图象交于点P (x0, 6) . 当x0 ≤x ≤3时, 求平移后的二次函数y的取值范围.
的图象交于点P (x0, 6) . 当x0 ≤x ≤3时, 求平移后的二次函数y的取值范围.
1.(1)∵A(a, -3)在![]() 的图象上,
的图象上,
∴![]() .
.
解得![]() . ……………………………………1分
. ……………………………………1分
∴反比例函数的解析式为![]() .
.
2.(2)过A作AC⊥y轴于C.
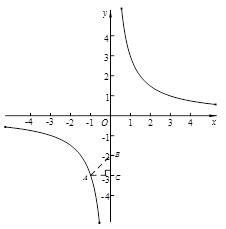 ∵ A(-1, -3),
∵ A(-1, -3),
∴ AC=1,OC=3.
∵ ∠ABO=135°,
∴ ∠ABC=45°.
可得 BC=AC=1.
∴ OB=2.
∴ B (0, -2). …………………3分
由抛物线![]() 与y轴交于B,得c= -2.
与y轴交于B,得c= -2.
∵a= -1,
∴![]() .
.
∵ 抛物线过A(-1,-3),
∴ ![]() .
.
∴ b=0.
∴ 二次函数的解析式为![]() .
.
3.(3)将![]() 的图象沿x轴翻折,得到二次函数解析式为
的图象沿x轴翻折,得到二次函数解析式为![]() . ……………5分
. ……………5分
设将![]() 的图象向右平移后的二次函数解析式为
的图象向右平移后的二次函数解析式为![]() (m>0).
(m>0).
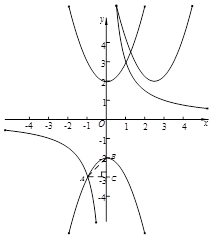 ∵ 点P(x0, 6)在函数
∵ 点P(x0, 6)在函数![]() 上,
上,
∴![]()
∴![]() .
.
∴![]() 的图象过点
的图象过点![]() .
.
∴![]() .
.
可得![]() (不合题意,舍去).
(不合题意,舍去).
∴ 平移后的二次函数解析式为![]() . …………………………6分
. …………………………6分
∵ a=1>0,
∴ 当![]() 时,
时,![]() ; 当
; 当![]() 时,
时,![]() .
.
∴ 当![]() 时,
时,![]() . ……………………………………7分
. ……………………………………7分
∴ 平移后的二次函数y的取值范围为 ![]() .
.
解析:略

练习册系列答案
相关题目
已知二次函数y=ax+bx+c(a≠0,a,b,c为常数),对称轴为直线x=1,它的部分自变量与函数值y的对应值如下表,写出方程ax2+bx+c=0的一个正数解的近似值________(精确到0.1).
| x | -0.1 | -0.2 | -0.3 | -0.4 |
| y=ax2+bx+c | -0.58 | -0.12 | 0.38 | 0.92 |
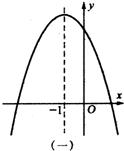 21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
21、已知二次函数y=a(x+1)2+c的图象如图所示,则函数y=ax+c的图象只可能是( )
