题目内容
如图，AD是∠EAC的平分线，AD∥BC，∠B=30°，则∠C为（ ）
| A．30° | B．60° | C．80° | D．120° |
A．
解析试题分析：：∵AD∥BC，∠B=30°，
∴∠EAD=∠B=30°，
∵AD是∠EAC的平分线，
∴∠EAC=2∠EAD=2×30°=60°，
∴∠C=∠EAC-∠B=60°-30°=30°．
故选A．
考点：1.平行线的性质；2.角平分线的性质．
练习册系列答案
相关题目
下面四个图形中，∠1与∠2是对顶角的图形（ ）
| A．甲 | B．乙 | C．丙 | D．丁 |
如图，AB∥ED，则∠A＋∠C＋∠D＝( )
| A．180° | B．270° | C．360° | D．540° |
如图，AB=AC， AD∥BC，∠BAC=100°，则∠CAD的度数是（ ）
| A．30° | B．35° | C．40° | D．50° |
下列说法中正确的是（ ）
| A．两直线被第三条直线所截得的同位角相等 |
| B．两直线被第三条直线所截得的同旁内角互补 |
| C．两平行线被第三条直线所截得的同位角的平分线互相垂直 |
| D．两平行线被第三条直线所截得的同旁内角的平分线互相垂直 |
如图，点
在
的延长线上，下列条件中能判断AB//CD的是（ ）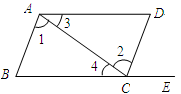
| A．∠3=∠4 | B．∠D=∠DCE |
| C．∠B=∠D | D．∠1=∠2 |
下列命题为真命题的是( )
| A．平面内任意三点确定一个圆 |
| B．五边形的内角和为540° |
| C．如果a>b，则ac2>bc2 |
| D．如果两条直线被第三条直线所截，那么所截得的同位角相等 |