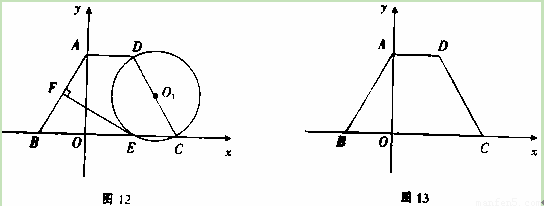题目内容
(本小题13分)如图,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 和直线
和直线![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() .
.
![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 求经过点
求经过点![]() 、
、![]() 、
、![]() 的抛物线的解析式;
的抛物线的解析式;
![]() 在抛物线上是否存在
在抛物线上是否存在![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
. ![]()
![]() ;
;![]()
![]() ;
;![]()
![]() 、
、![]() 、
、![]()
解析: ![]() 如图,易知
如图,易知![]() 、
、![]() ,设直线
,设直线![]() 的解析式为:
的解析式为:![]() ,则
,则
 所以,直线
所以,直线![]() 的解析式为
的解析式为![]()
![]() 设经过点
设经过点![]() 、
、![]() 、
、![]() 的抛物线的解析式为:
的抛物线的解析式为:![]() ,则
,则
 ,所以经过点
,所以经过点![]() 、
、![]() 、
、![]() 的抛物线的解析式为:
的抛物线的解析式为:![]()
![]() 设存在点
设存在点![]() ,坐标为
,坐标为![]() ,则
,则![]()
又![]() ,
,
![]() ,所以,
,所以,![]()
![]()
把![]() 分别代入
分别代入![]() ,得
,得![]()
由:![]()
由:![]()
![]()
所以![]() 的坐标为:
的坐标为:![]() 、
、![]() 、
、![]()
【关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ),B(-2,0).
),B(-2,0).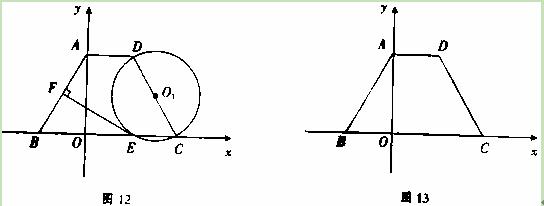
 ),B(-2,0).
),B(-2,0).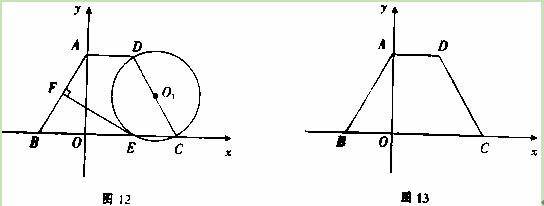
 是矩形,点
是矩形,点 的坐标为
的坐标为 ,直线
,直线 和直线
和直线 相交于点
相交于点 ,点
,点 是
是 的中点,
的中点, ,垂足为
,垂足为 .
. 求直线
求直线 求经过点
求经过点 、
、 的抛物线的解析式;
的抛物线的解析式; 在抛物线上是否存在
在抛物线上是否存在 ,使得
,使得 ,若存在,求出点
,若存在,求出点 ),B(-2,0).
),B(-2,0).