题目内容
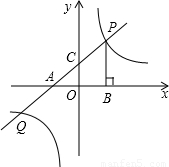
已知，如图D、E分别是△ABC的边AB、AC上的点，DE∥BC，且S△ADE：S四边形DBCE=1：15，那么DE：BC的值等于| 1 |
| 4 |
| 1 |
| 4 |
分析：由于DE∥BC，那么△ADE∽△ABC，根据S△ADE：S四边形DBCE=1：15易求S△ADE：S△ABC=1：16，结合相似三角形的面积比等于相似比的平方，易求DE：BC的值．
解答：解：∵DE∥BC，
∴△ADE∽△ABC，
∵S△ADE：S四边形DBCE=1：15，
∴S△ADE：S△ABC=1：16，
又∵S△ADE：S△ABC=（
）2，
∴
=
．
故答案是
．
∴△ADE∽△ABC，
∵S△ADE：S四边形DBCE=1：15，
∴S△ADE：S△ABC=1：16，
又∵S△ADE：S△ABC=（
| DE |
| BC |
∴
| DE |
| BC |
| 1 |
| 4 |
故答案是
| 1 |
| 4 |
点评：本题考查了相似三角形的判定和性质，解题的关键是根据平行线分线段成比例定理的推论得出△ADE∽△ABC．
练习册系列答案
相关题目
已知：如图，直线y=-x+4分别与x轴，y轴交于A、B两点，从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是（ ）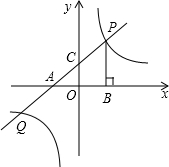
曲线
已知：如图，EF分别交于AB、CD于E、F，∠AEF=∠EFD，EG平分∠AEF，FH平分∠EFD．试说明EG∥FH成立的理由．
分别交
，
于点
，
，且∠AEF=
，
的平分线与
的平分线相交于点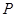
．
，求
的度数．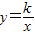
在第一象限内的交点，PB⊥x轴，垂足为点B，△APB的面积为6．