题目内容
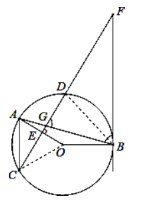
【题目】如图,在![]() 中,弦
中,弦![]() 与弦
与弦![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() ,过点
,过点![]() 的直线与
的直线与![]() 的延长线交于点
的延长线交于点![]() ,
,![]() .
.
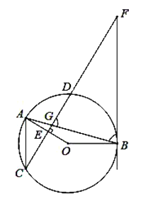
(1)若![]() ,求证:
,求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,请用
,请用![]() 表示
表示![]() 的半径;
的半径;
(3)求证:![]() .
.
【答案】(1)见解析;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据等边对等角可得∠OAB=∠OBA,然后根据OA⊥CD得到∠OAB+∠AGC=90°推出∠FBG+∠OBA=90°,从而得到OB⊥FB,再根据切线的定义证明即可;
(2)根据两直线平行,内错角相等可得∠ACF=∠F,根据垂径定理可得![]() ,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
,连接OC,设圆的半径为r,表示出OE,然后利用勾股定理列式计算即可求出r;
(3)连接BD,根据在同圆或等圆中,同弧所对的圆周角相等可得∠DBG=∠ACF,然后求出∠DBG=∠F,从而求出△BDG和△FBG相似,根据相似三角形对应边成比例列式表示出BG2,然后代入,整理等式左边即可得证.
(1)∵![]()
∴![]() ,
,
∵![]() ,
,
∴![]()
又∵![]() ,
,![]() ,
,
∴![]()
即![]() ,
,
∴![]()
∴![]() 是
是![]() 的切线;
的切线;
(2)∵![]() ,
,![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,即
,即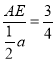 ,
,
解得![]() ,
,
连接![]() ,设圆的半径为
,设圆的半径为![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ;
;
(3)证明:连接![]() ,
,
∵![]() ,
,![]() (已证)
(已证)
∴![]()
又∵![]() ,
,
∴![]()
∴![]()
即![]() ,
,
∴![]() ,
,
即![]() .
.

练习册系列答案
相关题目
【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有![]() 本,最多的有
本,最多的有![]() 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:
本数(本) | 频数(人数) | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|

(![]() )统计图表中的
)统计图表中的![]() __________,
__________,![]() __________,
__________,![]() __________.
__________.
(![]() )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.
(![]() )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.
(![]() )若该校八年级共有
)若该校八年级共有![]() 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读![]() 本及以上的人数.
本及以上的人数.