题目内容
已知：如图，平行四边形ABCD中，AB=12，AB边上的高为3，BC边上的高为6，求平行四边形ABCD的周长为________．
36
分析：首先根据平行四边形的面积求法：DF×AB=CB×DE，求出BC长，再根据平行四边形的性质得到AD=BC=6，AB=CD=12，即可得到答案．
解答：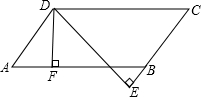
解：∵AB=12，
∴平行四边形的面积为：AB×DF=12×3=36，
∴BC×DE=36，
∴BC=36÷6=6，
∵四边形ABCD是平行四边形，
∴AD=BC=6，AB=CD=12，
∴平行四边形ABCD的周长=12+12+6+6=36．
故答案为：36．
点评：此题主要考查了平行四边形的面积公式与平行四边形的性质，解题的关键是利用面积公式求出未知边的长．
分析：首先根据平行四边形的面积求法：DF×AB=CB×DE，求出BC长，再根据平行四边形的性质得到AD=BC=6，AB=CD=12，即可得到答案．
解答：
解：∵AB=12，∴平行四边形的面积为：AB×DF=12×3=36，
∴BC×DE=36，
∴BC=36÷6=6，
∵四边形ABCD是平行四边形，
∴AD=BC=6，AB=CD=12，
∴平行四边形ABCD的周长=12+12+6+6=36．
故答案为：36．
点评：此题主要考查了平行四边形的面积公式与平行四边形的性质，解题的关键是利用面积公式求出未知边的长．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
