题目内容
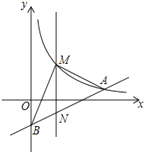
【题目】如图，在平面直角坐标系中，已知点A（8，1），B（0，﹣3），反比例函数y=
（x＞0）的图象经过点A，动直线x=t（0＜t＜8）与反比例函数的图象交于点M，与直线AB交于点N．
（1）k的值是______；
（2）当t=4时，求△BMN面积．
【答案】8
【解析】(1)、根据点A的坐标得出k的值；(2)、利用待定系数法求出直线AB的解析式，然后得出MN的长度，根据铅锤×水平÷2得出三角形的面积．
（1）把点A（8，1）代入反比例函数y=
（x＞0），
得：k=1×8=8，即k=8；
（2）设直线AB的解析式为：y=ax+b，根据题意得：
，解得：
，
∴直线AB的解析式为：y=
x﹣3； 当t=4时，M（4，2），N（4，﹣1），则MN=3，
∴△BMN的面积=×3×4=6.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
