题目内容
若矩阵A=
,B=
,则mA=
.
AB=
.
例如:
=
=
如果A=
,则2个A的乘积A2= ;5个的乘积A5= .
|
|
|
AB=
|
例如:
|
|
|
|
如果A=
|
分析:根据题中的新定义将所求式子化为普通运算,计算即可得到结果.
解答:解:根据题意得:A2=
=
=
;
∵A4=
=
,
A5=
=
=
.
故答案为:
;
|
|
|
|
∵A4=
|
|
|
A5=
|
|
|
|
|
|
故答案为:
|
|
点评:此题考查了有理数的混合运算,属于新定义题型,熟练掌握题中的新定义是解本题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
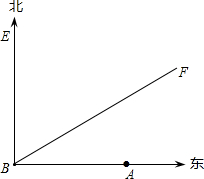 如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域.
如图,A城气象台测得台风中心在A城正西方向320km的B处,以每小时40km的速度向北偏东60°的BF方向移动,距离台风中心200km的范围内是受台风影响的区域. 13、如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=
13、如图,在△ABC中,AB=AC,AB的中垂线交AB于点D,交BC的延长线于点E,交AC于点F,若∠A=50°,AB+BC=6,则△BCF的周长=