题目内容
边长为1的正五边形的边心距为( )A.

B.

C.

D.

【答案】分析:本题应作出辅助线,构造出直角三角形来解决.
解答: 解:经过正五边形的中心O作边AB的垂线OC,则∠BOC=36°,那么∠OBC=54°;
解:经过正五边形的中心O作边AB的垂线OC,则∠BOC=36°,那么∠OBC=54°;
在直角△OBC中,根据三角函数得到OC=BC•tan54°= tan54°.
tan54°.
故选C.
点评:正多边形的计算一般要经过中心作边的垂线,并连接中心与一个端点构造直角三角形,把正多边形的计算转化为解直角三角形的问题.
解答:
 解:经过正五边形的中心O作边AB的垂线OC,则∠BOC=36°,那么∠OBC=54°;
解:经过正五边形的中心O作边AB的垂线OC,则∠BOC=36°,那么∠OBC=54°;在直角△OBC中,根据三角函数得到OC=BC•tan54°=
 tan54°.
tan54°.故选C.
点评:正多边形的计算一般要经过中心作边的垂线,并连接中心与一个端点构造直角三角形,把正多边形的计算转化为解直角三角形的问题.

练习册系列答案
相关题目
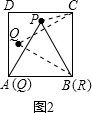
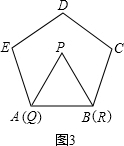
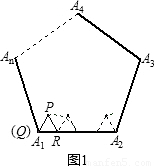
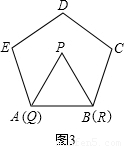
 27、阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.
27、阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.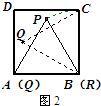

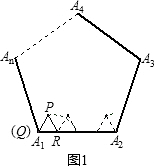 阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.
阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.