题目内容
在直径为1000mm的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=800mm，则油的最大深度为 mm．
【答案】分析：本题是已知圆的直径，弦长求油的最大深度其实就是弧AB的中点到弦AB的距离，可以转化为求弦心距的问题，利用垂径定理来解决．
解答：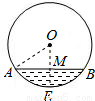
解：过点O作OM⊥AB交AB于M，交弧AB于点E．连接OA．
在Rt△OAM中：OA=500mm，AM=
AB=400mm．
根据勾股定理可得OM=300mm，则油的最大深度ME为200mm．
点评：圆中的有关半径，弦长，弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题．
解答：
解：过点O作OM⊥AB交AB于M，交弧AB于点E．连接OA．在Rt△OAM中：OA=500mm，AM=
AB=400mm．根据勾股定理可得OM=300mm，则油的最大深度ME为200mm．
点评：圆中的有关半径，弦长，弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题．
练习册系列答案
名校课堂系列答案
相关题目
在直径为1000mm的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=800mm，则油的最大深度为
