题目内容
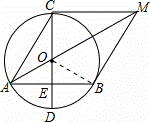
如图,已知AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E,且点E是OD的中点,⊙O的切线BM与AO的延长线相交于点M,连接AC,CM.
(1)若AB=4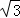 ,求
,求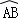 的长;(结果保留π)
的长;(结果保留π)
(2)求证:四边形ABMC是菱形.

(1)解:∵OA=OB,E为AB的中点,
∴∠AOE=∠BOE,OE⊥AB,
∵OE⊥AB,E为OD中点,
∴OE=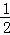 OD=
OD=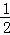 OA,
OA,
∴在Rt△AOE中,∠OAB=30°,∠AOE=60°,∠AOB=120°,
设OA=x,则OE=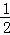 x,AE=
x,AE=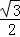 x,
x,
∵AB=4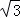 ,
,
∴AB=2AE=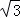 x=4
x=4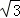 ,
,
解得:x=4,
则 的长l=
的长l=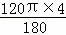 =
=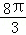 ;
;
(2)证明:由(1)得∠OAB=∠OBA=30°,∠BOM=∠COM=60°,∠AMB=30°,
∴∠BAM=∠BMA=30°,
∴AB=BM,
∵BM为圆O的切线,
∴OB⊥BM,
在△COM和△BOM中,
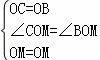 ,
,
∴△COM≌△BOM(SAS),
∴CM=BM,∠CMO=∠BMO=30°,
∴CM=AB,∠CMO=∠MAB,
∴CM∥AB,
∴四边形ABMC为菱形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是  ,并在数轴上表示不等式组的解集.
,并在数轴上表示不等式组的解集. 何体的俯视图是( )
何体的俯视图是( )
 B.
B. C.
C. D.
D.
 点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到
点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到 线段BN.
线段BN.
 的相反数是( )
的相反数是( ) +(﹣3)0=
+(﹣3)0=