题目内容
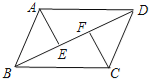
【题目】如图①所示,![]() 是某公园的平面示意图,
是某公园的平面示意图,![]() 分别是该公园的四个入口,两条主干道
分别是该公园的四个入口,两条主干道![]() 交于点
交于点![]() ,经测量
,经测量![]() ,
,![]() ,
,![]() ,请你帮助公园的管理人员解决以下问题:
,请你帮助公园的管理人员解决以下问题:
(1)公园的面积为 ![]() ;
;
(2)如图②,公园管理人员在参观了武汉东湖绿道后,为提升游客游览的体验感,准备修建三条绿道![]() ,其中点
,其中点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() (点
(点![]() 与点
与点![]() 不重合),并计划在
不重合),并计划在![]() 与
与![]() 两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
两块绿地所在区域种植郁金香,求种植郁金香区域的面积;
(3)若修建(2)中的绿道每千米费用为10万元,请你画出该公园修建这三条绿道投入资金最小值时的图形.
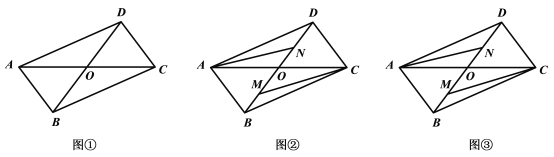
【答案】(1)![]() (2)
(2)![]() (3)见解析
(3)见解析
【解析】
(1)根据平行四边形的性质求得![]() 、
、![]() ,添加辅助线
,添加辅助线![]() ,从而求得
,从而求得![]() 的面积,进一步即可得解;
的面积,进一步即可得解;
(2)根据已知条件可知![]() ,从而将所求
,从而将所求![]() 的值转化为求
的值转化为求![]() 的值即可得解;
的值即可得解;
(3)本题是研究![]() 最短时的
最短时的![]() 、
、![]() 的取法,而
的取法,而![]() 是定值,所以问题集中在研究
是定值,所以问题集中在研究![]() 最小上。但
最小上。但![]() 、
、![]() 不能衔接,可将
不能衔接,可将![]() 平移
平移![]() 处,则
处,则![]() 可转化为
可转化为![]() ,要使
,要使![]() 最短,显然,
最短,显然,![]() 、
、![]() 、
、![]() 三点要在同一条直线上。
三点要在同一条直线上。
解:(1)∵四边形![]() 是平行四边形
是平行四边形
∴![]() ,
,![]()
∴在![]() 中,过点
中,过点![]() 作
作![]() 于点
于点![]() ,如图:
,如图:
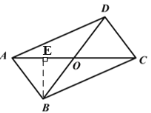
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴![]() .
.
(2)连接![]() 、
、![]() ,如图:
,如图:
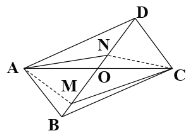
∵在![]() 中,
中,![]()
∴![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∴种植郁金香区域的面积为![]() .
.
(3)将![]() 沿
沿![]() 向下平移
向下平移![]() 至
至![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,此时点
,此时点![]() 位于点
位于点![]() 处,此时即为
处,此时即为![]() 取最小值,如图:
取最小值,如图:

故答案是:(1)![]() (2)
(2)![]() (3)见解析
(3)见解析

练习册系列答案
相关题目