题目内容
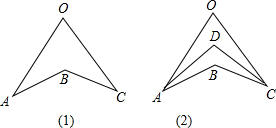
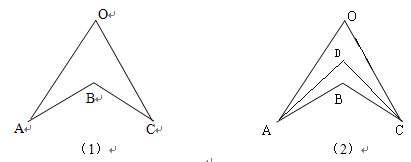
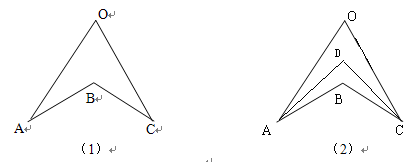
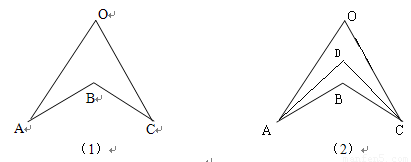
如图(1),由三角形的内角和或外角和可知:∠ABC=∠A+∠C+∠O在图(2)中,直接利用上述的结论探究:
①若AD、CD分别平分∠OAB,∠OCB,且∠O=80°∠B=120°,求∠ADC的度数
②AD、CD分别平分∠OAB,∠OCB,猜想∠O,∠ABC,∠ADC之间的等量关系,并说明理由.

 解:①根据题意得:∠OAB+∠OCB=∠B-∠O=120°-80°=40°,
解:①根据题意得:∠OAB+∠OCB=∠B-∠O=120°-80°=40°,∵AD、CD分别平分∠OAB,∠OCB,
∴∠OAD+∠OCD=
 ×40°=20°,
×40°=20°,∴∠ADC=∠O+∠OAD+∠OCD=80°+20°=100°;
②如图,作射线OD,
根据三角形的外角的性质得:∠ABE=∠ADB+∠DAB,∠CBE=∠CDB+∠DCB,
∵∠ADB=∠AOD+∠DAO,∠CDB=∠COD+∠DCO,
∴∠ABE=∠ADB+∠AOB,∠CBE=∠CDB+∠COB,
∴∠ABC=∠ADC+∠O.
分析:利用三角形的内角和和三角形的外角的性质列出算式后等量代换即可得到答案.
点评:此题主要考查了三角形内角和定理以及角平分线的定义,由于图中涉及的角较多,理清角之间的关系是解决问题的关键.

练习册系列答案
相关题目