题目内容
如图，点O是菱形ABCD对角线的交点，过点C作BD的平行线CE，过点D作AC的平行线DE，CE与DE相交于点E，试说明四边形OCED是矩形．分析：要证明四边形OCED是矩形，由已知知其为平行四边形，又由菱形对角线互相垂直，得出其一个角为直角，即为所求结论．
解答：证明：∵DE∥AC，CE∥BD，
∴DE∥OC，CE∥OD
∴四边形OCED是平行四边形，
又∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠COD=90°，
∴四边形OCED是矩形．
∴DE∥OC，CE∥OD
∴四边形OCED是平行四边形，
又∵四边形ABCD是菱形，
∴AC⊥BD，
∴∠COD=90°，
∴四边形OCED是矩形．
点评：解决问题的关键是熟练掌握矩形的性质及判定定理．
练习册系列答案
高效智能课时作业系列答案
相关题目
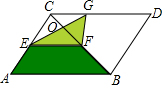如图，点F是菱形ABDC对角线BC上一动点，EF∥AB，GF∥AC，菱形两条对角线BC和AD的长分别为2cm、5cm，当点F在BC上移动时，阴影面积会改变吗？如果不变，请求出阴影部分的面积．
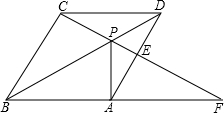长线于F．
（2013•苏州）如图，点P是菱形ABCD对角线AC上的一点，连接DP并延长DP交边AB于点E，连接BP并延长交边AD于点F，交CD的延长线于点G．
