题目内容
【题目】(本题共12分)如图,在平面直角坐标系中,顶点为![]() 的抛物线交
的抛物线交![]() 轴于
轴于![]() 点,交
点,交![]() 轴于
轴于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧).已知
的左侧).已知![]() 点坐标为
点坐标为![]() .
.
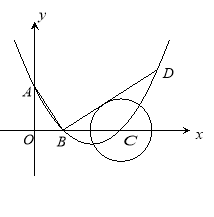
(1)求此抛物线的解析式;
(2) 过点![]() 作线段
作线段![]() 的垂线交抛物线于点
的垂线交抛物线于点![]() , 如果以点
, 如果以点![]() 为圆心的圆与直线
为圆心的圆与直线![]() 相切,请判断抛物线的对称轴
相切,请判断抛物线的对称轴![]() 与
与![]() 有怎样的位置关系,并给出证明;
有怎样的位置关系,并给出证明;
(3)已知点![]() 是抛物线上的一个动点,且位于
是抛物线上的一个动点,且位于![]() ,
,![]() 两点之间,问:当点
两点之间,问:当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?并求出此时
的面积最大?并求出此时![]() 点的坐标和
点的坐标和![]() 的最大面积.
的最大面积.
【答案】(1)![]() ;(2)相交;过程见解析;(3)△PAC的面积最大值为
;(2)相交;过程见解析;(3)△PAC的面积最大值为![]() ;点
;点![]() 的坐标为
的坐标为![]() .
.
【解析】
试题分析:
(1)首先将抛物线的解析式设成顶点式,然后将点![]() 的坐标代入求出函数解析式;
的坐标代入求出函数解析式;
(2)首先根据函数解析式求出点![]() 和点
和点![]() 的坐标,从而得出
的坐标,从而得出![]() 的长度,然后设圆
的长度,然后设圆![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,根据题意得出
,根据题意得出![]() 和
和![]() 相似,从而得出
相似,从而得出![]() 的长度,然后得出答案;
的长度,然后得出答案;
(3)过点![]() 作
作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,求出
,求出![]() 的解析式,根据函数解析式分别设出点
的解析式,根据函数解析式分别设出点![]() 和点
和点![]() 的坐标,求出
的坐标,求出![]() 的长度,然后将
的长度,然后将![]() 的面积用含
的面积用含![]() 的代数式表示出来,从而根据函数的性质得出最大值.
的代数式表示出来,从而根据函数的性质得出最大值.
试题解析:
解:(1)设抛物线为![]() .
.
∵抛物线经过点![]() ,
,
∴![]() .
.
∴![]() .
.
∴抛物线为![]() ........(2分)
........(2分)
(2)![]() 与
与![]() 相交.
相交.
当![]() 时,
时,![]() ,
,![]() .
.
∴![]() 为
为![]() ,
,![]() 为
为![]() ........(2分)
........(2分)
∴![]() .
.
设![]() 与
与![]() 相切于点
相切于点![]() ,连接
,连接![]() ,则
,则![]() .
.
∵![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]()
∴![]() .
.
∴![]() .
.
∴![]() ........(3分)
........(3分)
∵抛物线的对称轴![]() 为
为![]() ,
,
∴![]() 点到
点到![]() 的距离为
的距离为![]() .
.
∴抛物线的对称轴![]() 与
与![]() 相交........(5分)
相交........(5分)
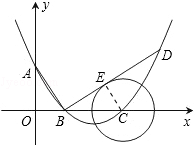
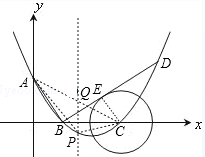
(3)过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() .
.
根据题意可得:![]() 的解析式为
的解析式为![]() ........(1分)
........(1分)
设![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),则
),则![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ).
).
∴![]() .
.
∵![]() ........(3分)
........(3分)
∴当![]() 时,
时,![]() 的面积最大为
的面积最大为![]() ........(4分)
........(4分)
此时,![]() 点的坐标为
点的坐标为![]() ........(5分)
........(5分)

练习册系列答案
相关题目
