题目内容
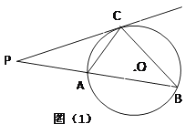
【题目】已知,如图(1), ![]() 为⊙
为⊙![]() 的割线,直线
的割线,直线![]() 与⊙
与⊙![]() 有公共点
有公共点![]() , 且
, 且![]() ,
,
(1)求证: ![]() ; 直线
; 直线![]() 是⊙
是⊙![]() 的切线;
的切线;
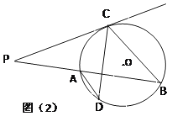
(2)如图(2) , 作弦![]() ,使
,使![]() 连接AD、BC,若
连接AD、BC,若![]() ,求⊙
,求⊙![]() 的半径;
的半径;
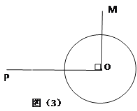
(3)如图(3),若⊙![]() 的半径为
的半径为![]() ,
,![]() ,
,![]() ,
,![]() ,⊙
,⊙![]() 上是否存在一点
上是否存在一点![]() , 使得
, 使得![]() 有最小值?若存在,请求出这个最小值;若不存在,说明理由。
有最小值?若存在,请求出这个最小值;若不存在,说明理由。
【答案】(1) 证明见解析; 证明见解析; (2) R=![]() ;(3)
;(3)![]() 最小值为
最小值为![]()
【解析】试题分析:(1)根据已知条件得到![]() ,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;
,推出△PCA∽△PBC,根据相似三角形的性质得到∠PCA=∠PBC,作直径CF,连接AF,则∠CAF=90°,得到∠PCA+∠FCA=90°,P过直径的一端点C,于是得到结论;
(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,推出AE∥CD,得到![]() ,根据勾股定理得到BE=2
,根据勾股定理得到BE=2![]() ,于是得到结论;
,于是得到结论;
(3)取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,连接QO、QM,得到OG=![]() OM=1,根据相似三角形的性质得到
OM=1,根据相似三角形的性质得到![]() ,求得QG=
,求得QG=![]() QM,根据两点之间线段最短,即可得到结论.
QM,根据两点之间线段最短,即可得到结论.
试题解析:(1)①证明:∵PC2=PA×PB,
∴![]() ,
,
∵∠CPA=∠BPC,
∴△PCA∽△PBC,
∴∠PCA=∠PBC,
②作直径CF,连接AF,则∠CAF=90°,

∴∠F+∠FCA=90°,
∵∠F=∠B,∠PCA=∠PBC,
∴∠PCA+∠FCA=90°,
∵PC经过直径的一端点C,
∴直线PC是⊙O的切线;
(2)作直径BE,连接CE、AE.则∠BCE=∠BAE=90°,
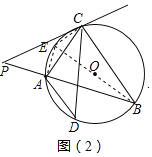
∵CD⊥AB,
∴AE∥CD,
∴![]() ,
,
∴AD=CE=2,
∵BC=6,
∴在Rt△BCE中,由勾股定理得:
BE2=CE2+BC2=22+62=40,
∴BE=2![]() ,
,
∴R=![]() ;
;
(3)取OM中点G,连接PG与⊙O的交点就是符合条件的点Q,连接QO、QM,
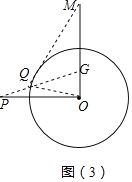
∵MO=2,
∴OG=![]() OM=1,
OM=1,
∵⊙O的半径r=OQ=![]() ,
,
∴OQ2=OGOM,
∵∠MOQ=∠QOG,
∴△MOQ∽△QOG,
∴![]() ,
,
∴QG=![]() QM,
QM,
∴PQ+![]() QM=PQ+QG=PG,
QM=PQ+QG=PG,
根据两点之间线段最短,
此时PQ+![]() QM=PQ+QG=PG最小,
QM=PQ+QG=PG最小,
∴PQ+![]() QM最小值为PG=
QM最小值为PG=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案