Question

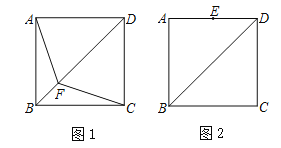
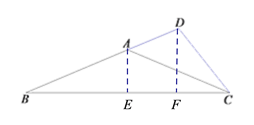
【题目】如图，在等腰三角形ABC中，AB=AC，点D在BA的延长线上，BC=24， ．

（1）求AB的长；

（2）若AD=6.5，求的余切值．

Answer 1

【答案】（1）13（2）

【解析】试题分析：

（1）过点A作AE⊥BC于点E，结合AB=AC，BC=24可得BE=12，在Rt△AEB中，由sin∠ABC= 设AE=5k，AB=13k，由勾股定理可得解得BE=12k=12，由此可得k=1，从而可得AB=13；

（2）过点D作DF⊥BC于点F，则易得BD=19.5，AE∥DF，从而可得结合AE=5，BE=12，AB=13即可求得DF=，BF=18，由此可得CF=BC-BF=6，结合∠DFC=90°即可得到cot∠DCB= .

试题解析：

（1）过点A作AE⊥BC，垂足为点E，

∵AB=AC，

∴BE=BC=12，

在Rt△ABE中，∠AEB=90°，sin∠ABC=，

设AE=5k，AB=13k，∵AB2=AE2+BE2，

∴169k2=25k2+BE2，解得BE=12K=12，

∴k=1，

∴AE=5，AB=13；

（2）过点D作DF⊥BC，垂足为点F，

∵AD=6.5，AB=13，

∴BD=AB+AD=19.5，

∵AE⊥BC，DF⊥BC ，

∴ ∠AEB=∠DFB=90°，

∴AE∥DF，

∴，

又 ∵ AE=5，BE=12，AB=13，

∴DF=，BF=18，

∴CF=BC=BF=6，

∵在Rt△DCF中，∠DFC=90°，

∴cot∠DCB= .