题目内容
 如图,Rt△ABC≌Rt△A′B′C′,∠A=∠A′=30°.观察分析图形,把你发现的正确结论至少写出三个.
如图,Rt△ABC≌Rt△A′B′C′,∠A=∠A′=30°.观察分析图形,把你发现的正确结论至少写出三个.BC=B′C′,∠B=∠B′,AC′=A′C(答案不唯一)
BC=B′C′,∠B=∠B′,AC′=A′C(答案不唯一)
.分析:根据全等三角形对应边相等,对应角相等,直角三角形30°角所对的直角边等于斜边的一半解答即可.
解答:解:∵Rt△ABC≌Rt△A′B′C′,
∴AC=A′C′,AB=A′B′,BC=B′C′,∠B=∠B′,
∴AC-CC′=A′C′-CC′,
即AC′=A′C,
∵∠A=∠A′=30°,
∴BC=
AB,B′C′=
A′B′,
所以,正确的结论有:AC=A′C′,AB=A′B′,BC=B′C′,∠B=∠B′,AC′=A′C,BC=
AB,B′C′=
A′B′(任写三个即可).
故答案为:BC=B′C′,∠B=∠B′,AC′=A′C(答案不唯一).
∴AC=A′C′,AB=A′B′,BC=B′C′,∠B=∠B′,
∴AC-CC′=A′C′-CC′,
即AC′=A′C,
∵∠A=∠A′=30°,
∴BC=
| 1 |
| 2 |
| 1 |
| 2 |
所以,正确的结论有:AC=A′C′,AB=A′B′,BC=B′C′,∠B=∠B′,AC′=A′C,BC=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:BC=B′C′,∠B=∠B′,AC′=A′C(答案不唯一).
点评:本题考查了全等三角形的性质,30°角所对的直角边等于斜边的一半的性质,是基础题,熟记性质是解题的关键,是开放型题目,答案不唯一.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过
如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过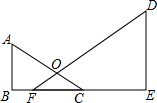 已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15.
已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15. (2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6
(2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6