Question

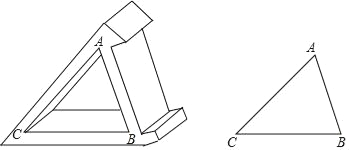
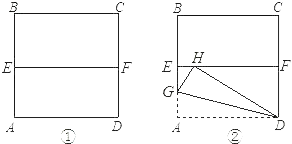
【题目】在一次测量活动中，同学们要测量某公园的码头A与他正东方向的亭子B之间的距离，如图他们选择了与码头A、亭子B在同一水平面上的点P在点P处测得码头A位于点P北偏西方向30°方向，亭子B位于点P北偏东43°方向；又测得P与码头A之间的距离为200米，请你运用以上数据求出A与B的距离．

Answer 1

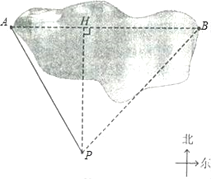
【答案】262米

【解析】

过P作AB的垂线，设垂足为H．在Rt△APH中求出AH、PH的长，进而在Rt△PHB中求得BH的长；由AB=AH+BH即可求出A、B间的距离．

解：作PH⊥AB于点H．

则∠APH=30°，

在Rt△APH中，

AH=100，PH=APcos30°=100．

Rt△PBH中，

BH=PHtan43°≈161.60．

AB=AH+BH≈262．

答：码头A与B的距离约为262米．