题目内容
在锐角△ABC中，AD⊥BC，D为垂足，DE⊥AC，E为垂足，DF⊥AB，F为垂足．O为△ABC的外心．求证：（1）△AEF∽△ABC；（2）AO⊥EF．
分析：（1）利用直角三角形相似，得出有关比例式，再利用两边对应成比例，且夹角相等，可以证明．
（2）利用圆周及定理以及（1）中结论，要证垂直，应证另两角互余．
（2）利用圆周及定理以及（1）中结论，要证垂直，应证另两角互余．
解答：
（1）证明：∵AD⊥BC，DE⊥AC，DF⊥AB，
∴Rt△ADB∽Rt△AFD，Rt△ADC∽Rt△AED，
∴
=
，即：AD2=AB•AF，
=
，即：AD2=AE•AC，
∴AB•AF=AE•AC，
即：
=
，
又∵∠BAC=∠BAC，
∴△AEF∽△ABC；
（2）证明：连接AO并延长到⊙O上一点M，连接BM，
∵AM是圆的直径，
∴∠ABM=∠M+∠BAM=90°，
又∵∠C+∠CAD=90°，∠C=∠M，
∴∠BAM=∠CAD，
∵△AEF∽△ABC，
∴∠C=∠AFE，
∴∠AFE+∠BAM=90°，
即：AO⊥EF．
（1）证明：∵AD⊥BC，DE⊥AC，DF⊥AB，∴Rt△ADB∽Rt△AFD，Rt△ADC∽Rt△AED，
∴
| AD |
| AF |
| AB |
| AD |
| AD |
| AE |
| AC |
| AD |
∴AB•AF=AE•AC，
即：
| AB |
| AE |
| AC |
| AF |
又∵∠BAC=∠BAC，
∴△AEF∽△ABC；
（2）证明：连接AO并延长到⊙O上一点M，连接BM，
∵AM是圆的直径，
∴∠ABM=∠M+∠BAM=90°，
又∵∠C+∠CAD=90°，∠C=∠M，
∴∠BAM=∠CAD，
∵△AEF∽△ABC，
∴∠C=∠AFE，
∴∠AFE+∠BAM=90°，
即：AO⊥EF．
点评：此题主要考查了相似三角形的判定，以及圆周角定理，综合性较强，有利于同学们综合能力的提高．
练习册系列答案
相关题目
在锐角△ABC中，a、b、c分别表示为∠A、∠B、∠C的对边，O为其外心，则O点到三边的距离之比为（ ）
| A、a：b：c | ||||||
B、
| ||||||
| C、cosA：cosB：cosC | ||||||
| D、sinA：sinB：sinC |
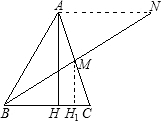在锐角△ABC中，最大的高线AH等于中线BM，求证：∠B＜60°（如图）．
如图，在锐角△ABC中，∠BAC=60°，BD、CE为高，F为BC的中点，连接DE、DF、EF，则结论：①B、E、D、C四点共圆；②AD•AC=AE•AB；③△DEF是等边三角形；④当∠ABC=45°时，BE=
（2013•南开区一模）在锐角△ABC中，∠BAC=60°，BD、CE为高，F是BC的中点，连接DE、EF、FD，则以下结论中一定正确的个数有（ ）