Question

【题目】我市为开发沿黄流域小白河渔业资源，鼓励养殖户开展混合养殖，现公布如下政策:每亩水面年租金为元；每亩水面可在年初混合投放公斤甲种鱼和公斤乙种鱼:经市场调查发现:每公斤甲种鱼的价格为元，每公斤甲种鱼的饲养费用为元，每公斤甲种鱼当年可获元收益；每公斤乙种鱼的价格为元，每公斤乙种鱼的饲养费用为元，每公斤乙种鱼当年可获元收益；

（1）某养殖户现有资金元，他准备再向银行贷款，用于甲乙鱼混合养殖，已知银行贷款的年利率为，试问该养殖户至少应租多少亩水面，并至少向银行贷款多少元，可使年利润不少于元？

（2）为了节省材料该养殖户利用河岸的一角的两边为边，用总长为米的围网在水库中围成了如图所示的①②③三块区域，其中区域①为直角三角形，区域②③为矩形，而且四边形为直角梯形．

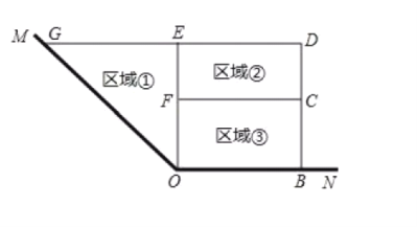
I．若①②③这块区域的面积相等，则的长为 米；

II．设四边形的面积为求与之的函数关系式，并说明为何值时，有最大值？最大值是多少？

Answer 1

【答案】（1）该养殖户至少应租亩水面，至少向银行贷款元；（2）I；II当时，有最大值，最大值为．

【解析】

（1）首先根据题目计算得出混合养殖的利润(每亩的年利润)，再设应该租x亩水面，根据年利润减去银行贷款利息大于等于36600列出不等式求解即可；

（2）I．利用一元二次方程求解即可；II．由已知得出，继而得出，可得出四边形的面积为，化为顶点式，即可得出答案．

解：苗种费用(元)

饲养费(元)

成本(元)

收益(元)

利润(每亩的年利润)(元)

设该养殖户应租亩水面．

根据题意列出不等式:，

解得:．

则该养殖户至少应租亩水面，至少向银行贷款元

答:该养殖户至少应租亩水面，至少向银行贷款元．

由题意可知，

，，

设

则

I．这块区域的面积相等，

或(舍弃)，

．

答:当这块区域的面积相等时长米．

II． 由题意可知，，，

，

则

四边形的面积为，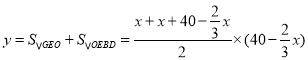

整理得

且

当时，有最大值，最大值为．