题目内容
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.(1)求x的取值范围;
(2)若△ABC为直角三角形,求x的值;
(3)探究:△ABC的最大面积?

【答案】分析:(1)因为所求AB或x在△ABC中,所以可利用三角形三边之间的关系即两边之和大于第三边,两边之差小于第三边进行解答.
(2)应该分情况讨论,因为不知道在三角形中哪一个是作为斜边存在的.所以有三种情况,即:①若AC为斜边,则1=x2+(3-x)2,即x2-3x+4=0,无解.
②若AB为斜边,则x2=(3-x)2+1,解得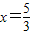 ,满足1<x<2.
,满足1<x<2.
③若BC为斜边,则(3-x)2=1+x2,解得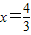 ,满足1<x<2.
,满足1<x<2.
∴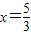 或
或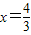 .
.
(3)在△ABC中,AB的值固定不变,即可视为底边不变,但是因为三角形形状不固定,
高在发生变化,所以造成面积不固定,需分情况进行讨论.具体分①若点D在线段AB上,②若点D在线段MA上两种情况.
解答:解:(1)∵在△ABC中,AC=1,AB=x,BC=3-x.
∴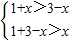 ,
,
解得1<x<2;
(2)①若AC为斜边,则1=x2+(3-x)2,即x2-3x+4=0,无解,
②若AB为斜边,则x2=(3-x)2+1,解得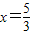 ,满足1<x<2,
,满足1<x<2,
③若BC为斜边,则(3-x)2=1+x2,解得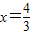 ,满足1<x<2,
,满足1<x<2,
∴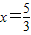 或
或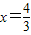 ;
;
(3)在△ABC中,作CD⊥AB于D,
设CD=h,△ABC的面积为S,则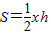 ,
,
①若点D在线段AB上,
则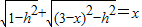 ,
,
∴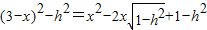 ,
,
即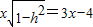 ,
,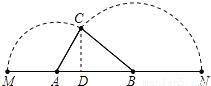
∴x2(1-h2)=9x2-24x+16,
即x2h2=-8x2+24x-16.
∴S2= x2h2=-2x2+6x-4=-2(x-
x2h2=-2x2+6x-4=-2(x- )2+
)2+ (
( ≤x<2),
≤x<2),
当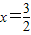 时(满足
时(满足 ≤x<2)S2取最大值
≤x<2)S2取最大值 ,从而S取最大值
,从而S取最大值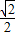 ;
;
②若点D在线段MA上,
则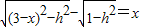 ,
,
同理可,得
S2= x2h2=-2x2+6x-4
x2h2=-2x2+6x-4
=-2(x- )2+
)2+ (1<x≤
(1<x≤ ),
),
易知此时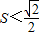 ,
,
综合①②得,△ABC的最大面积为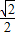 .
.
点评:解此题的关键是进行全方面分析,注意一题多解.难易程度适中.
(2)应该分情况讨论,因为不知道在三角形中哪一个是作为斜边存在的.所以有三种情况,即:①若AC为斜边,则1=x2+(3-x)2,即x2-3x+4=0,无解.
②若AB为斜边,则x2=(3-x)2+1,解得
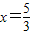 ,满足1<x<2.
,满足1<x<2.③若BC为斜边,则(3-x)2=1+x2,解得
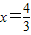 ,满足1<x<2.
,满足1<x<2.∴
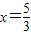 或
或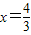 .
.(3)在△ABC中,AB的值固定不变,即可视为底边不变,但是因为三角形形状不固定,
高在发生变化,所以造成面积不固定,需分情况进行讨论.具体分①若点D在线段AB上,②若点D在线段MA上两种情况.
解答:解:(1)∵在△ABC中,AC=1,AB=x,BC=3-x.
∴
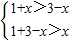 ,
,解得1<x<2;
(2)①若AC为斜边,则1=x2+(3-x)2,即x2-3x+4=0,无解,
②若AB为斜边,则x2=(3-x)2+1,解得
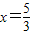 ,满足1<x<2,
,满足1<x<2,③若BC为斜边,则(3-x)2=1+x2,解得
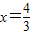 ,满足1<x<2,
,满足1<x<2,∴
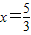 或
或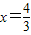 ;
;(3)在△ABC中,作CD⊥AB于D,
设CD=h,△ABC的面积为S,则
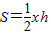 ,
,①若点D在线段AB上,
则
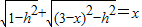 ,
,∴
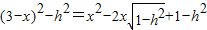 ,
,即
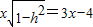 ,
,
∴x2(1-h2)=9x2-24x+16,
即x2h2=-8x2+24x-16.
∴S2=
 x2h2=-2x2+6x-4=-2(x-
x2h2=-2x2+6x-4=-2(x- )2+
)2+ (
( ≤x<2),
≤x<2),当
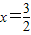 时(满足
时(满足 ≤x<2)S2取最大值
≤x<2)S2取最大值 ,从而S取最大值
,从而S取最大值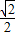 ;
;②若点D在线段MA上,
则
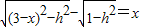 ,
,同理可,得
S2=
 x2h2=-2x2+6x-4
x2h2=-2x2+6x-4=-2(x-
 )2+
)2+ (1<x≤
(1<x≤ ),
),易知此时
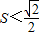 ,
,综合①②得,△ABC的最大面积为
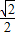 .
.点评:解此题的关键是进行全方面分析,注意一题多解.难易程度适中.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
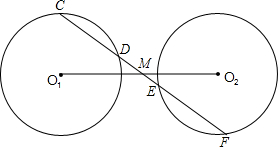 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母) 18、如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC.
18、如图,已知E、F是?ABCD对角线AC上的两点,且BE⊥AC,DF⊥AC. 如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线.
如图,已知∠AOC与∠BOC是邻补角,OD是∠AOC的角平分线,OE是∠BOC的平分线. 如图,已知P、Q是△ABC的边BC上的两点,BQ=CP,若不增加任何字母与辅助线,要使△ABP≌△ACQ,则还需增加一个条件是
如图,已知P、Q是△ABC的边BC上的两点,BQ=CP,若不增加任何字母与辅助线,要使△ABP≌△ACQ,则还需增加一个条件是 几何基础问题
几何基础问题