Question

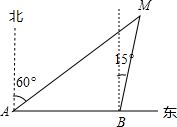如图，已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以28海里/时的速度向正东方向航行，半小时后到达B处，在B处看见灯塔M在北偏东15°方向，此时灯塔M与渔船的距离是（　　）

• A、7

  2

  海里
• B、14

  2

  海里
• C、7海里
• D、14海里

Answer 1

分析：过点B作BN⊥AM于点N，由已知可求得BN的长；再根据三角函数求BM的长．

解答：解：由已知得，AB=

1

2

×28=14海里，∠A=30°，∠ABM=105°．
过点B作BN⊥AM于点N．
∵在直角△ABN中，∠BAN=30°
∴BN=

1

2

AB=7海里．
在直角△BNM中，∠MBN=45°，则直角△BNM是等腰直角三角形．即BN=MN=7海里，
∴BM=

BN2+MN2

=

72+72

=7

2

海里．
故选A．

点评：解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的问题，解决的方法就是作高线．