题目内容
 (2012•江西)如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.
(2012•江西)如图,等腰梯形ABCD放置在平面直角坐标系中,已知A(-2,0)、B(6,0)、D(0,3),反比例函数的图象经过点C.(1)求点C坐标和反比例函数的解析式;
(2)将等腰梯形ABCD向上平移m个单位后,使点B恰好落在双曲线上,求m的值.
分析:(1)过点C作CE⊥AB于点E,根据HL证Rt△AOD≌Rt△BEC,求出OA=BE=2,即可求出C的坐标,代入反比例函数的解析式求出k即可;
(2)得出B′的坐标是(6,m),代入反比例函数的解析式,即可求出答案.
(2)得出B′的坐标是(6,m),代入反比例函数的解析式,即可求出答案.
解答:解:(1)过点C作CE⊥AB于点E,
∵四边形ABCD是等腰梯形,
∴AD=BC,DO=CE,
∵∠DOA=∠CEO=90°,
在Rt△AOD和Rt△BEC中
∵
,
∴Rt△AOD≌Rt△BEC(HL),
∴AO=BE=2,
∵BO=6,
∴DC=OE=4,
∴C(4,3),
∵设反比例函数的解析式y=
(k≠0),
根据题意得:3=
,
解得k=12,
∴反比例函数的解析式y=
;
答:点C坐标是(4,3),反比例函数的解析式是y=
.
(2)将等腰梯形ABCD向上平移m个单位后得到梯形A′B′C′D′,
∴点B′(6,m),
∵点B′(6,m)恰好落在双曲线y=
上,
∴当x=6时,y=
=2,
即m=2.

∵四边形ABCD是等腰梯形,
∴AD=BC,DO=CE,
∵∠DOA=∠CEO=90°,
在Rt△AOD和Rt△BEC中
∵
|
∴Rt△AOD≌Rt△BEC(HL),
∴AO=BE=2,
∵BO=6,
∴DC=OE=4,
∴C(4,3),
∵设反比例函数的解析式y=
| k |
| x |
根据题意得:3=
| k |
| 4 |
解得k=12,
∴反比例函数的解析式y=
| 12 |
| x |
答:点C坐标是(4,3),反比例函数的解析式是y=
| 12 |
| x |
(2)将等腰梯形ABCD向上平移m个单位后得到梯形A′B′C′D′,
∴点B′(6,m),
∵点B′(6,m)恰好落在双曲线y=
| 12 |
| x |
∴当x=6时,y=
| 12 |
| 6 |
即m=2.
点评:本题考查了用待定系数法求反比例函数的解析式,反比例函数图象上点的坐标特征,全等三角形的性质和判定,等腰梯形的性质的应用,通过做此题培养学生运用性质进行计算的能力,题型较好,难度也适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2012•江西)如图,AC经过⊙O的圆心O,AB与⊙O相切于点B,若∠A=50°,则∠C=
(2012•江西)如图,AC经过⊙O的圆心O,AB与⊙O相切于点B,若∠A=50°,则∠C=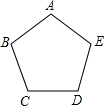 (2012•江西) 如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
(2012•江西) 如图,已知正五边形ABCDE,请用无刻度的直尺,准确地画出它的一条对称轴(保留作图痕迹).
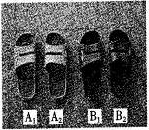 (2012•江西)如图,大小、质地相同,仅颜色不同的两双拖鞋(分左、右脚)共四只,放置在地板上[可表示为(A1,A2),(B1,B2)].
(2012•江西)如图,大小、质地相同,仅颜色不同的两双拖鞋(分左、右脚)共四只,放置在地板上[可表示为(A1,A2),(B1,B2)]. (2012•江西)如图,已知二次函数L1:y=x2-4x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.
(2012•江西)如图,已知二次函数L1:y=x2-4x+3与x轴交于A、B两点(点A在点B的左边),与y轴交于点C.