Question

【题目】如图，在中，，AC=4，BC=3，O是AB上一点，且AO:OB=2:5，过点O作垂足为D，

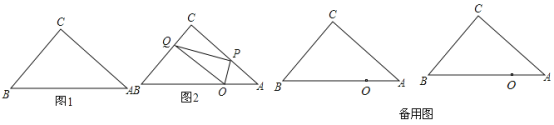
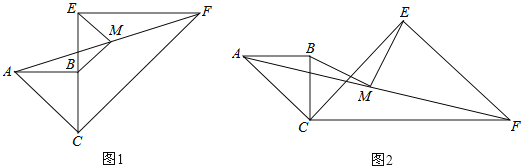
（1）求点O到直线AC的距离OD的长；（图1）

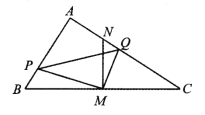
（2）若P是边AC上的一个动点，作交线段BC于Q（不与B、C重合）（图2）

①求证：；

②设，，试求关于的函数解析式，并写出定义域；

③若与相似，求的长度.

Answer 1

【答案】（1）；（2）①见解析；②；③或

【解析】

（1）首先作，判断出，推得，即可判断出；然后根据，求出OD的长度，就是点O到AC的距离；
（2）①根据同角的余角相等得到，然后利用相似三角形的判定定理证明；
②由（1）可知，求出AD、PD的长度各是多少，然后根据，即可推得，据此求出y关于x的函数解析式，并写出函数定义域即可；
③根据题意，分两种情况：当时，当PQ平分时，分类讨论，根据②中函数解析式和角平分线的性质，分别求出AP长是多少即可.

解：（1）如图1，作，

∵，
∴，
∵，，
∴，
∴，
∴，
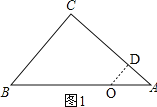
又∵，
∴，
解得，
即点O到AC的距离是；
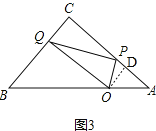
（2）①如图3，作，

∵，
∴，
又∵，
∴，
在和△QPC中， ，
∴；
②如图3，作，

，，
∴，
∴，
∴，
又∵，
∴，
解得，，
∵，
∴，
∴，
∴；
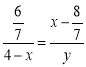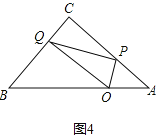
③如图4，当时，与相似，

∵，
∴，
∴，
解得，
∴，
解得或，
如图5，作于点E，

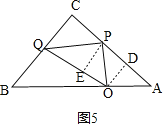
当PQ平分时，，
∵，，，
∴，
∵，，
∴，
又∵，，
∴，
∴，
即点P为CD的中点,
由，可得，
解得，
综上可得：当与相似时，、或.