Question

【题目】定义：若某抛物线上有两点A、B关于原点对称，则称该抛物线为“完美抛物线”．已知二次函数y=ax2﹣2mx+c（a，m，c均为常数且ac≠0）是“完美抛物线”：
（1）试判断ac的符号；
（2）若c=﹣1，该二次函数图象与y轴交于点C，且S△ABC=1．
①求a的值；
②当该二次函数图象与端点为M（﹣1，1）、N（3，4）的线段有且只有一个交点时，求m的取值范围．

Answer 1

【答案】
（1）

解：设A （p，q）．则B （﹣p，﹣q），

把A、B坐标代入解析式可得： ，

∴2ap2+2c=0．即 ，

∴ ，

∵ac≠0，

∴ ，

∴ac＜0

（2）

解：∵c=﹣1，

∴ ，a＞0，且C（0，﹣1），

∴ ，

①S△ABC= ×2 ×1=1，

∴a=1；

②由①可知：抛物线解析式为y=x2﹣2mx﹣1，

∵M（﹣1，1）、N（3，4）．

∴MN： （﹣1≤x≤3），

依题，只需联立 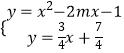在﹣1≤x≤3内只有一个解即可，

∴x2﹣2mx﹣1= x+ ，

故问题转化为：方程x2﹣（2m+ ）x﹣ =0在﹣1≤x≤3内只有一个解，

建立新的二次函数：y=x2﹣（2m+ ）x﹣ ，

∵△=（2m+ ）2+11＞0且c=﹣ ＜0，

∴抛物线 与x轴有两个交点，且交y轴于负半轴．

不妨设方程 的两根分别为x1，x2．（x1＜x2）

则

∵方程 在﹣1≤x≤3内只有一个解．

故分两种情况讨论：

（Ⅰ）若﹣1≤x1＜3且x2＞3：则 ．即： ，

可得： ．

（Ⅱ）若x1＜﹣1且﹣1＜x2≤3：则 ．即： ，

可得： ，

综上所述， 或

【解析】（1）设A （p，q）．则B （﹣p，﹣q），把A、B坐标代入解析式可得方程组即可得到结论；（2）由c=﹣1，得到 ，a＞0，且C（0，﹣1），求得 ，①根据三角形的面积公式列方程即可得到结果；②由①可知：抛物线解析式为y=x2﹣2mx﹣1，根据M（﹣1，1）、N（3，4）．得到这些MN的解析式 （﹣1≤x≤3），联立方程组得到x2﹣2mx﹣1= x+ ，故问题转化为：方程x2﹣（2m+ ）x﹣ =0在﹣1≤x≤3内只有一个解，建立新的二次函数：y=x2﹣（2m+ ）x﹣ ，根据题意得到（Ⅰ）若﹣1≤x1＜3且x2＞3，（Ⅱ）若x1＜﹣1且﹣1＜x2≤3：列方程组即可得到结论．