题目内容
【题目】如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA︰AC=2︰5,直线CD垂直于直线AB于点P,交x轴于点D。
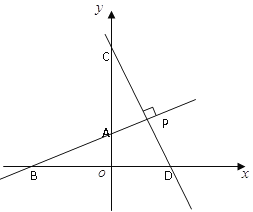
(1)求出点A、点B的坐标。
(2)请求出直线CD的解析式。
【答案】(1)A(0,2),B(-4,0)
(2)D(![]() ,0),yCD=-2x+7
,0),yCD=-2x+7
【解析】(1)∵x2-6x+8=0
∴x1=4,x2=2
∵0A、0B为方程的两个根,且0A<0B
∴0A=2,0B=4
∴ A(0,2),B(-4,0)
(2) ∵ 0A:AC=2:5
∴ AC=5
∴OC=OA+AC=2+5=7
∴ C(0,7)
∵∠BAO=∠CAP,∠CPB=∠BOA=90O
∴∠PBD=∠OCD
∵∠ BOA=∠COD=90O
∴△BOA∽△COD
∴![]() =
=![]()
∴ OD=![]() =
=![]() =
=![]()
∴D(![]() ,0)
,0)
设直线 CD的解析式为y=KX+b,
把x=0,y=7;x=![]() ,y=0分别代入得:
,y=0分别代入得: 
解得![]()
∴yCD=-2x+7

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
