题目内容
受国际炒家炒作的影响,今年棉花价格出现了大幅度波动.1至3月份,棉价大幅度上涨,其价格y1 (元/吨)与月份x 之间的函数关系式为:y1=2200x+24200(1≤ ≤3,且
≤3,且 取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份
取整数).而从4月份起,棉价大幅度走低,其价格y2(元/吨)与月份 (4≤x≤6,且x取整数)之间的函数关系如图所示.
(4≤x≤6,且x取整数)之间的函数关系如图所示.
(1)直接写出棉价y2 (元/吨)与月份 之间所满足的一次函数关系式;
之间所满足的一次函数关系式;
(2)某棉被厂今年1至3月份的棉花进货量p1 (吨)与月份x之间所满足的函数关系式为:p1=-10x+170 (1≤x≤3,且 取整数);4至6月份棉花进货量p2(吨)与月份
取整数);4至6月份棉花进货量p2(吨)与月份 之间所满足的函数关系式为p2=40x-20
(4≤
之间所满足的函数关系式为p2=40x-20
(4≤ ≤6,且
≤6,且 取整数).求在前6个月中该棉被厂的棉花进货金额最大的月份和该月的进货金额;
取整数).求在前6个月中该棉被厂的棉花进货金额最大的月份和该月的进货金额;
(3)经厂方研究决定,若7月份棉价继续下降,则对棉花进行收储.若棉价在6月份的基础上下降a%,则该厂7月份进货量在6月份的基础上增加2 %.若要使7月份进货金额为5130400元,请你估算出
%.若要使7月份进货金额为5130400元,请你估算出 的最大整数值.
的最大整数值.
(参考数据:352=1225,362=1296,372=1369,382=1444)
解:(1) y2=-2000x+34000(4≤ ≤6,且
≤6,且 取整数).
取整数).
(2)在1到 月份中,设每月棉花的进货金额为
月份中,设每月棉花的进货金额为 (元),
(元),



 (≤
(≤ ≤
≤ ,且
,且 取整数).
取整数).
∵ ,∴第3月份的进货金额最大,其最大金额为
,∴第3月份的进货金额最大,其最大金额为

 元.
元.
在 到
到 月份中,设每月棉花的进货金额为
月份中,设每月棉花的进货金额为 (元),
(元),


 (
( ≤
≤ ≤
≤ ,且
,且 取整数).
取整数).
∵
 ,而当
,而当 ≤
≤ ≤
≤ 时,
时, 随
随 的增大而增大,
的增大而增大,
∴第 月份的进货金额最大,其最大金额为
月份的进货金额最大,其最大金额为

 元.
元.
∵4312000<4840000, ∴在前6个月中,第6月份棉被厂的棉花进货金额最大,
最大金额为4840000元.
(3) 月份的进货量为p2=40×6-20=220(吨),
月份的进货量为p2=40×6-20=220(吨),
棉价为 y2=-2000×6+34000=22000 (元/吨) ,
由题意得 .
.
令 ,整理得
,整理得
 ,
,
解得  .
.
∵ ,
, ,而1269更接近1300,∴取
,而1269更接近1300,∴取 .
.
∴ 或
或 .
.
∵所求为最大整数值,∴ 取
取

答: 的最大整数值为
的最大整数值为 .
.
【解析】(1)用待定系数法求得棉价y2
(元/吨)与月份 之间所满足的一次函数关系式
之间所满足的一次函数关系式
(2)求出1到 月份中每月棉花的进货金额
月份中每月棉花的进货金额 和
和 到
到 月份中每月棉花的进货金额
月份中每月棉花的进货金额 的关系式,进行讨论作比较
的关系式,进行讨论作比较
(3)通过 月份的进货量和棉价,列方程求解,估算
月份的进货量和棉价,列方程求解,估算 最大整数值
最大整数值

 该厂7月份进货量在6月份的基础上增加2a%.若要使7月份进货金额为5130400元,请你估算出a的最大整数值.
该厂7月份进货量在6月份的基础上增加2a%.若要使7月份进货金额为5130400元,请你估算出a的最大整数值. 该厂7月份进货量在6月份的基础上增加2a%.若要使7月份进货金额为5130400元,请你估算出a的最大整数值.
该厂7月份进货量在6月份的基础上增加2a%.若要使7月份进货金额为5130400元,请你估算出a的最大整数值.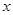 ≤3,且
≤3,且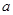 %.若要使7月份进货金额为5130400元,请你估算出
%.若要使7月份进货金额为5130400元,请你估算出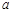 的最大整数值.
的最大整数值.