题目内容
11．
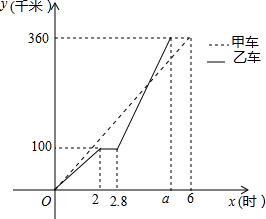甲、乙两车同时同时出发从A地前往B地，乙行驶途中有一次停车修理，修好后乙车的行驶速度是原来的2倍．两车距离A地的路程y（千米）与行驶时间x（时）的函数图象如图所示．（1）乙车到达B地所用的时间a的值为5.4；
（2）行驶过程中，两车出发多长时间首次后相遇？
（3）当x=3时，甲、乙两车之间的距离是60千米．
分析 （1）根据函数图象可以设出在2.8≤x≤a时乙车对应的函数解析式，从而可以求得a的值；
（2）根据函数图象求出在0≤x≤6时，甲车对应的函数解析式然后与乙车对应的函数解析式联立方程组，从而可以解答本题；
（3）将x=3分别代入甲车和乙车对应的函数解析式，从而可以解答本题．
解答 解：（1）当0≤x≤2时，设乙车在这段时间内对应的函数解析式为：y=kx．
∵点（2，100）在y=kx上，
∴100=2k，
得k=50，
∴当2.8≤x≤a时设乙车对应的函数解析式为：y=100x+b．
∵点（2.8，100）在y=100x+b上，
∴100=100×2.8+b，
解得，b=-180，
∴y=100x-180．
将y=360代入y=100x-180，得x=5.4．
即a的值是5.4．
故答案为：5.4．
（2）当0≤x≤6时，设甲车对应的函数的解析式为：y=mx
∵点（6，360）在y=mx上，
∴360=6m
得m=60
∴y=60x
由图象可知甲乙两车相遇在2.8≤x≤5.4之间
∴$\left\{\begin{array}{l}{y=60x}\\{y=100x-180}\end{array}\right.$
解得x=4.5，y=270
即行驶过程中，两车出发4.5小时时两车首次相遇
（3）将x=3代入y=60x得，y=180；
将x=3代入y=100x-180得，y=120．
180-120=60．
即当x=3时，甲、乙两车之间的距离是60千米．
故答案为：60．
点评 本题考查一次函数的应用，解题的关键是明确题意，利用数形结合的数学思想解答问题．
练习册系列答案
相关题目