题目内容
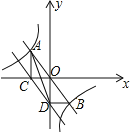
【题目】在平面直角坐标系内,抛物线![]() 与线段
与线段![]() 有两个不同的交点,其中点
有两个不同的交点,其中点![]() ,点
,点![]() .有下列结论:
.有下列结论:
①直线![]() 的解析式为
的解析式为![]() ;②方程
;②方程![]() 有两个不相等的实数根;③a的取值范围是
有两个不相等的实数根;③a的取值范围是![]() 或
或![]() .
.
其中,正确结论的个数为( )
A.0B.1C.2D.3
【答案】D
【解析】
①设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() ,点
,点![]() 代入即可得到答案;
代入即可得到答案;
②∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,令
有两个不同的交点,令![]() x+
x+![]() =ax2x+1,则
=ax2x+1,则![]() 即可得到结论;
即可得到结论;
③分a>0,a<0两种情况讨论,根据题意列出不等式组,可求a的取值范围.
解:①设直线![]() 的解析式为
的解析式为![]() ,把
,把![]() ,点
,点![]() 代入得,
代入得,
![]() 解得,
解得,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,故①正确;
,故①正确;
②∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,
有两个不同的交点,
令![]() x+
x+![]() =ax2x+1,则
=ax2x+1,则![]() ,
,
∴方程![]() 有两个不相等的实数根,故②正确;
有两个不相等的实数根,故②正确;
③∵抛物线![]() 与直线
与直线![]() 有两个不同的交点,
有两个不同的交点,
∴令![]() x+
x+![]() =ax2x+1,则2ax23x+1=0
=ax2x+1,则2ax23x+1=0
∴Δ=98a>0
∴a<![]()
a<0时,![]()
解得:a2
∴a2,
当a>0时,![]()
解得:a1
∴1a<![]()
综上所述:1a<![]() 或a2, 故③正确.
或a2, 故③正确.
故选:D.

练习册系列答案
相关题目