题目内容
已知直线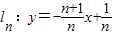 (n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
(n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线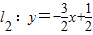 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,依此类推,直线ln与x轴和y轴分别交于点An和Bn,设△AnOBn的面积为Sn.
(1)求设△A1OB1的面积S1;
(2)求S1+S2+S3+…+S6的值.
【答案】分析:(1)因为当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,所以分别令y=0,x=0,即可求出A1和B1的坐标,从而求出△A1OB1的面积S1;
(2)要求S1+S2+S3+…+S6的值,需要找出Sn的规律,因为n=2时,y2=-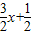 ,所以分别令y=0,x=0即可求出A2(
,所以分别令y=0,x=0即可求出A2( ,0),同理可求出A2,A3…所以推出当n=n时,yn=
,0),同理可求出A2,A3…所以推出当n=n时,yn=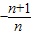 x+
x+ ,分别令y=0,x=0,即可求出An(
,分别令y=0,x=0,即可求出An(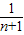 ,0),Bn(0,
,0),Bn(0,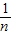 ),所以Sn=
),所以Sn= ,整理即可求出答案.
,整理即可求出答案.
解答:解:(1)∵y1=-2x+1,
∴A1( ,0),B1(0,1),
,0),B1(0,1),
∴S1=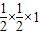 =
= ;
;
(2)∵y2=-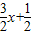 ,
,
∴A2( ,0),B2(0,
,0),B2(0, )
)
故S2= ,
,
∵y3=-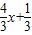 ,
,
∴A3( ,0),B3(0,
,0),B3(0, ),
),
故S3=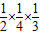 ,
,
…
∵yn=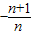 x+
x+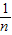 ,
,
∴An(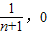 ),Bn(0,
),Bn(0,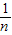 ),
),
故Sn=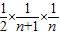 ,
,
∵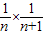 =
= ,
,
∴S1+S2+…+S6= (
(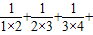 …
…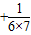 )
)
= [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(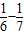 )]=
)]= (1-
(1- )=
)= .
.
点评:本题是一道推理性极强的题目,主要考查一次函数的基本的性质及特殊点的坐标,解题的关键是寻找规律.
(2)要求S1+S2+S3+…+S6的值,需要找出Sn的规律,因为n=2时,y2=-
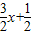 ,所以分别令y=0,x=0即可求出A2(
,所以分别令y=0,x=0即可求出A2( ,0),同理可求出A2,A3…所以推出当n=n时,yn=
,0),同理可求出A2,A3…所以推出当n=n时,yn=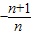 x+
x+ ,分别令y=0,x=0,即可求出An(
,分别令y=0,x=0,即可求出An(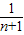 ,0),Bn(0,
,0),Bn(0,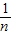 ),所以Sn=
),所以Sn= ,整理即可求出答案.
,整理即可求出答案.解答:解:(1)∵y1=-2x+1,
∴A1(
 ,0),B1(0,1),
,0),B1(0,1),∴S1=
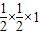 =
= ;
;(2)∵y2=-
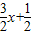 ,
,∴A2(
 ,0),B2(0,
,0),B2(0, )
)故S2=
 ,
,∵y3=-
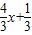 ,
,∴A3(
 ,0),B3(0,
,0),B3(0, ),
),故S3=
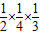 ,
,…
∵yn=
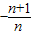 x+
x+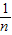 ,
,∴An(
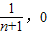 ),Bn(0,
),Bn(0,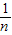 ),
),故Sn=
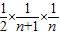 ,
,∵
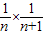 =
= ,
,∴S1+S2+…+S6=
 (
(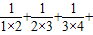 …
…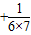 )
)=
 [(1-
[(1- )+(
)+( -
- )+…+(
)+…+(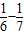 )]=
)]= (1-
(1- )=
)= .
.点评:本题是一道推理性极强的题目,主要考查一次函数的基本的性质及特殊点的坐标,解题的关键是寻找规律.

练习册系列答案
相关题目
 (n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
(n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,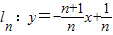 (n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
(n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线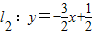 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2;…依此类推,直线ln与x轴和y轴分别交于点An和Bn,S1+S2+…+S2009的值是 .
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2;…依此类推,直线ln与x轴和y轴分别交于点An和Bn,S1+S2+…+S2009的值是 .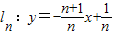 (n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
(n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线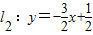 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,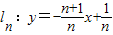 (n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线
(n是不为零的自然数).当n=1时,直线l1:y=-2x+1与x轴和y轴分别交于点A1和B1,设△A1OB1(其中O是平面直角坐标系的原点)的面积为S1;当n=2时,直线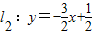 与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,
与x轴和y轴分别交于点A2和B2,设△A2OB2的面积为S2,…,