题目内容
已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离d可用公式d=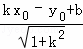 计算.
计算.
例如:求点P(﹣2,1)到直线y=x+1的距离.
解:因为直线y=x+1可变形为x﹣y+1=0,其中k=1,b=1.
所以点P(﹣2,1)到直线y=x+1的距离为d=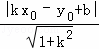 =
= =
= =
= .
.
根据以上材料,求:
(1)点P(1,1)到直线y=3x﹣2的距离,并说明点P与直线的位置关系;
(2)点P(2,﹣1)到直线y=2x﹣1的距离;
(3)已知直线y=﹣x+1与y=﹣x+3平行,求这两条直线的距离.
解:(1)∵点P(1,1),
∴点P到直线y=3x﹣2的距离为:
d= =0,
=0,
∴点P在直线y=3x﹣2上;
(2)由题意,得
∵y=2x﹣1
∴k=2,b=﹣1.
∵P(2,﹣1),
∴d= =
= .
.
∴点P(2,﹣1)到直线y=2x﹣1的距离为 ;
;
(3)在直线y=﹣x+1任意取一点P,
当x=0时,y=1.
∴P(0,1).
∵直线y=﹣x+3,
∴k=﹣1,b=3,
∴d= =
= ,
,
∴两平行线之间的距离为 .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
|
| A. | y=3(x+1)2+2 | B. | y=3(x+1)2﹣2 | C. | y=3(x﹣1)2+2 | D. | y=3(x﹣1)2﹣2 |
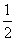 ,AB=
,AB=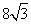 ,AG=
,AG=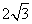 ,求BE的长;
,求BE的长;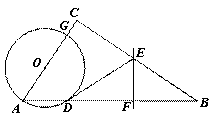 (3)若cosA=
(3)若cosA= )﹣2+(
)﹣2+( π﹣2014)0+sin60°+|
π﹣2014)0+sin60°+| ﹣2|.
﹣2|.
 B.
B.  C.
C.  D.
D. 

