题目内容
[阅读]在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
[运用]
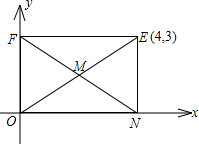
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为
(2)在直角坐标系中,有A(-1,2),B(3,1),C(1,4)三点,另有一点D与
 点A、B、C构成平行四边形的顶点,求点D的坐标.
点A、B、C构成平行四边形的顶点,求点D的坐标.
分析:(1)根据矩形的对角线互相平分及点E的坐标即可得出答案.
(2)根据题意画出图形,然后可找到点D的坐标.
(2)根据题意画出图形,然后可找到点D的坐标.
解答: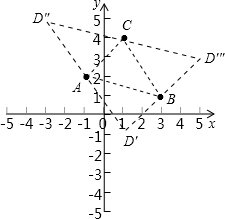 解:(1)M(
解:(1)M(
,
),即M(2,1.5).
(2)如图所示:
根据平行四边形的对角线互相平分可得:
设D点的坐标为(x,y),
∵以点A、B、C、D构成的四边形是平行四边形,
①当AB为对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴BC=
,
∴AD=
,
∵-1+3-1=1,2+1-4=-1,
∴D点坐标为(1,-1),
②当BC为对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴AC=2
,BD=2
,
D点坐标为(5,3).
③当AC为对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴AB=
,CD=
,
D点坐标为:(-3,5),
综上所述,符合要求的点有:D'(1,-1),D″(-3,5),D″′(5,3).
 解:(1)M(
解:(1)M(| 4+0 |
| 2 |
| 3+0 |
| 2 |
(2)如图所示:
根据平行四边形的对角线互相平分可得:
设D点的坐标为(x,y),
∵以点A、B、C、D构成的四边形是平行四边形,
①当AB为对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴BC=
| 13 |
∴AD=
| 13 |
∵-1+3-1=1,2+1-4=-1,
∴D点坐标为(1,-1),
②当BC为对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴AC=2
| 2 |
| 2 |
D点坐标为(5,3).
③当AC为对角线时,
∵A(-1,2),B(3,1),C(1,4),
∴AB=
| 17 |
| 17 |
D点坐标为:(-3,5),
综上所述,符合要求的点有:D'(1,-1),D″(-3,5),D″′(5,3).
点评:本题考查了平行四边形的性质及矩形的性质,关键是掌握已知两点求其中点坐标的方法.

练习册系列答案
相关题目
 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 点,这时点
点,这时点 与点
与点 为旋转中心时,点
为旋转中心时,点 点,点
点,点 点,点
点,点 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.


 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐为.
的坐为.