题目内容
在函数y=
(k<0)的图象上有A(1,y1)、B(-1,y2)、C(-2,y3)三个点,则下列各式中正确的是( )
| k |
| x |
分析:由k<0,根据反比例函数的性质得到函数y=
的图象分布在第二、四象限,在每一象限,y随x的增大而增大,而A(1,y1)在第四象限、B(-1,y2)和C(-2,y3)在第二象限,所以y1<0,y2>0,y3>0,且y2>y3,于是有y1<y3<y2.
| k |
| x |
解答:解:∵k<0,
∴函数y=
的图象分布在第二、四象限,在每一象限,y随x的增大而增大,
∴y1<0,y2>0,y3>0,且y2>y3,
∴y1<y3<y2.
故选B.
∴函数y=
| k |
| x |
∴y1<0,y2>0,y3>0,且y2>y3,
∴y1<y3<y2.
故选B.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k≠0)的图象上点的横纵坐标之积等于定值k.也考查了反比例函数的性质.
| k |
| x |

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
已知点(2,-6)在函数y=kx的图象上,则函数y=
的图象在( )
| k |
| x |
| A、第一、三象限 |
| B、第二、三象限 |
| C、第二、四象限 |
| D、第一、四象限 |
 如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数
如图,已知正方形OABC的面积为9,点O为坐标原点,点A在x轴上,点C在y轴上,点B在函数 如图,A、B两点在函数
如图,A、B两点在函数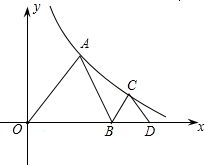 如图,△AOB和△BCD都是等边三角形,点A、C在函数
如图,△AOB和△BCD都是等边三角形,点A、C在函数