题目内容
如图1,AD是△ABC的角平分线,将△ABC折叠使点A落在点D处,折痕为EF,则四边形AEDF一定是( ).


| A.矩形 | B.菱形 | C.正方形 | D.梯形 |
B
分析:由△ABC折叠使点A落在点D处,折痕为EF,得到∠EAD=∠EDA,∠FAD=∠FDA,根据角平分线的性质推出∠FDA=∠EAD,∠FAD=∠EDA,证出平行四边形AEDF,根据折叠得到AD⊥EF,根据菱形的判定即可得出答案
解答:解:∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠FDA=∠EAD,∠FAD=∠EDA,
∴AE∥DF,DE∥AF,
∴四边形AEDF是平行四边形,
∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠AOE=∠DOE=90°,
即:AD⊥EF,
∴平行四边形AEDF是菱形.
故选B.
解答:解:∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵AD是△ABC的角平分线,
∴∠EAD=∠FAD,
∴∠FDA=∠EAD,∠FAD=∠EDA,
∴AE∥DF,DE∥AF,
∴四边形AEDF是平行四边形,
∵将△ABC折叠使点A落在点D处,折痕为EF,
∴∠AOE=∠DOE=90°,
即:AD⊥EF,
∴平行四边形AEDF是菱形.
故选B.

练习册系列答案
相关题目

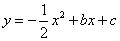 与x轴交于A(1,0)、
与x轴交于A(1,0)、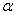 (0°<
(0°<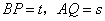 ,求s与t之间的函数关系式.
,求s与t之间的函数关系式.
 满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)
满分14分,第(1)小题4分,第(2)小题①6分、第(2)小题②4分)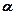 (
(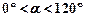 且
且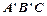 ,
,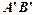 边经过点B时,求旋转角
边经过点B时,求旋转角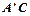 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥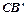 边于点E,联结BE.
边于点E,联结BE.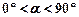 时,设
时,设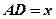 ,
,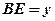 ,求
,求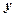 与
与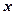 之间的函数解析式及定义域;
之间的函数解析式及定义域;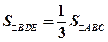 时,求
时,求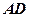 的长.
的长. 


 ,则这个正多边形的边数是________.
,则这个正多边形的边数是________.